一个博客

随便写写

0%

基于lowbit的二分查找

发表于 更新于

最近看了一下树状数组，想到之前头歌作业上的二分查找，然后就有了用lowbit实现二分查找的想法。

树状数组

树状数组的基本作用是单点修改和区间求和，它的核心就是一个lowbit函数。不过这次的重点不是树状数组，而是lowbit，它的作用是获取一个二进制数的最低位1。

1
#define lowbit(x) ((x)&(-x))

树状数组大概就是这个样子

如果要爬树那就是加上当前节点的lowbit

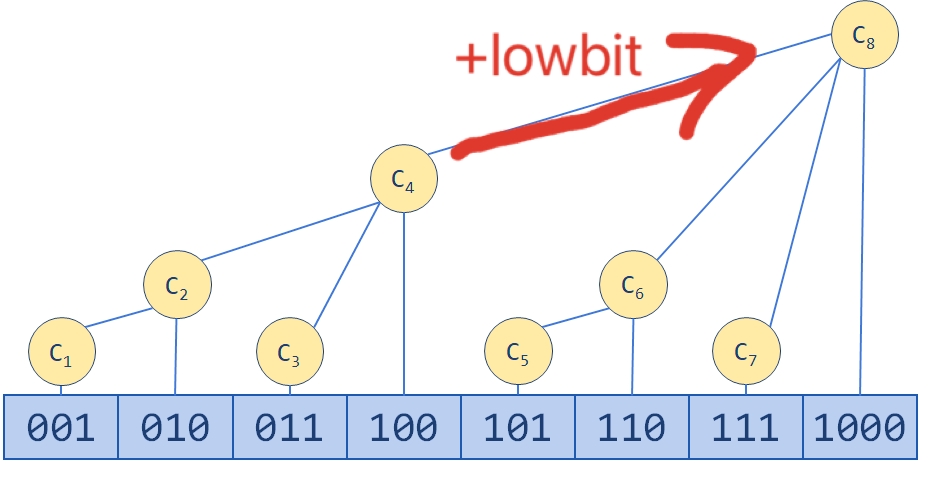
然后有一个我也不知道叫什么的操作，或许叫左跳和右跳吧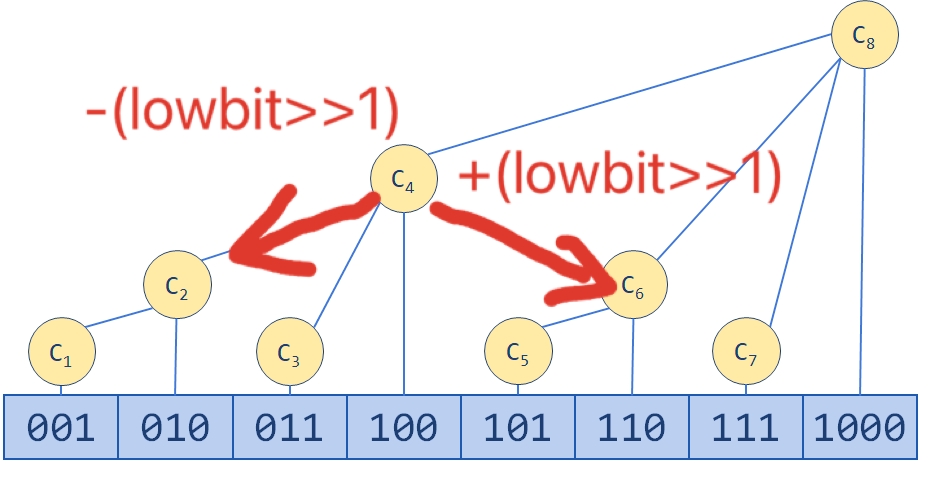

这个左右跳就是我想要用来实现二分查找的。

二分查找

普通的二分查找就不多说了，适用的条件是线性存储并且有序，这里也需要满足这些条件。

假设要在有n个数的有序数组A中找m，首先如果m大于A[n-1]，那就直接可以返回不存在。之后就是找到树顶和中间位置，如图

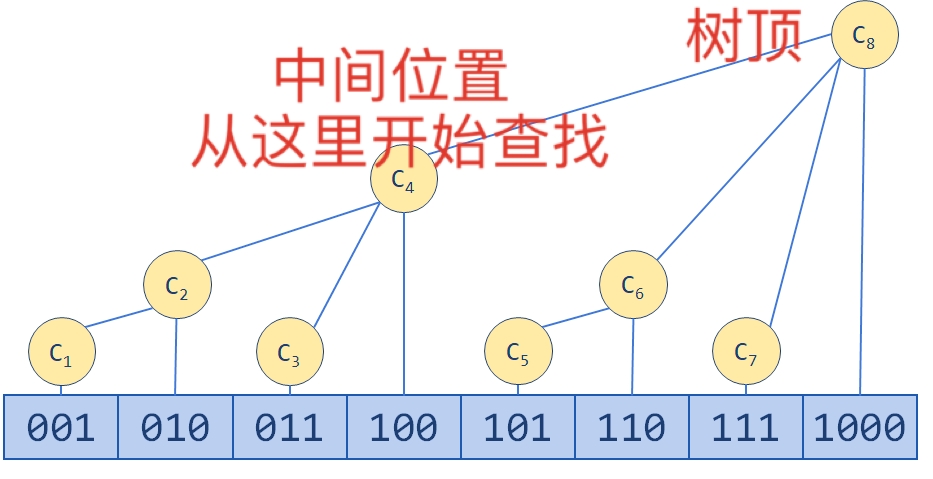
之后就和常规的二分查找一样了，大于就左跳，小于就右跳， 如果跳到底都没找到那就是不存在。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#define lowbit(x) ((x)&(-x))
int lowbit_search(int *A,int n,int m){
    if(m>A[n-1])return -1;
    int mid,top=n;
    while(top!=lowbit(top))top+=lowbit(top);
    mid=top>>1;
    while(lowbit(mid)!=1){
        if(A[mid]==m)return mid;
        if(A[mid]>m)mid-=lowbit(mid)>>1;
        else mid+=lowbit(mid)>>1;
    }
    if(A[mid]==m)return mid;
    return -1;
}

结尾

时间复杂度和普通二分查找一样都是$O(log_2n)$，可能常数还比二分查找大，写起来也比普通二分查找麻烦，理解上也比较复杂，所以我又写了个没用的算法。

如果对树状数组感兴趣的可以看看这个：算法学习笔记(2) : 树状数组