三分法求函数极小值

这题其实是我上matlab实验课时候的题目，我觉得有点意思，所以对这题有点印象，虽然还有一部分印象是老师说我逻辑混乱，所以记录一下这一题的写法。

题目解释

编写黄金分割法的程序，求函数$f(x)=x^2-3x-4,x\in [0,2]$的极小值，其中eps=0.001。黄金分割法算法:

给定区间[a,b]，及计算精度eps>0;

计算r=a+0.382(b-a)，u=a+0.618(b-a);

若f(r)>f(u)，转(4)，否则转(5)

若u-r<eps，则停，输出x=u,f=f(u)，否则令q=r, r=a+0.382(b-a), u=a+0.618(b-a)，转(3)。

若u-r<eps，则停，输出x=r,f=f(r)，否则令b=u, r=+0.382(b-a), u=a+0.618(b-a)，转(3)。

这题其实就是一个三分法求单峰函数极值的问题，思路跟二分逼近法很像，这个和一般三分法的区别是它是用黄金分割法来分的，接下来我用图片大概演示一下这个算法的过程。

首先在数轴上画出a,b,r,u和函数f的图像，并标出交点f(r),f(u)。

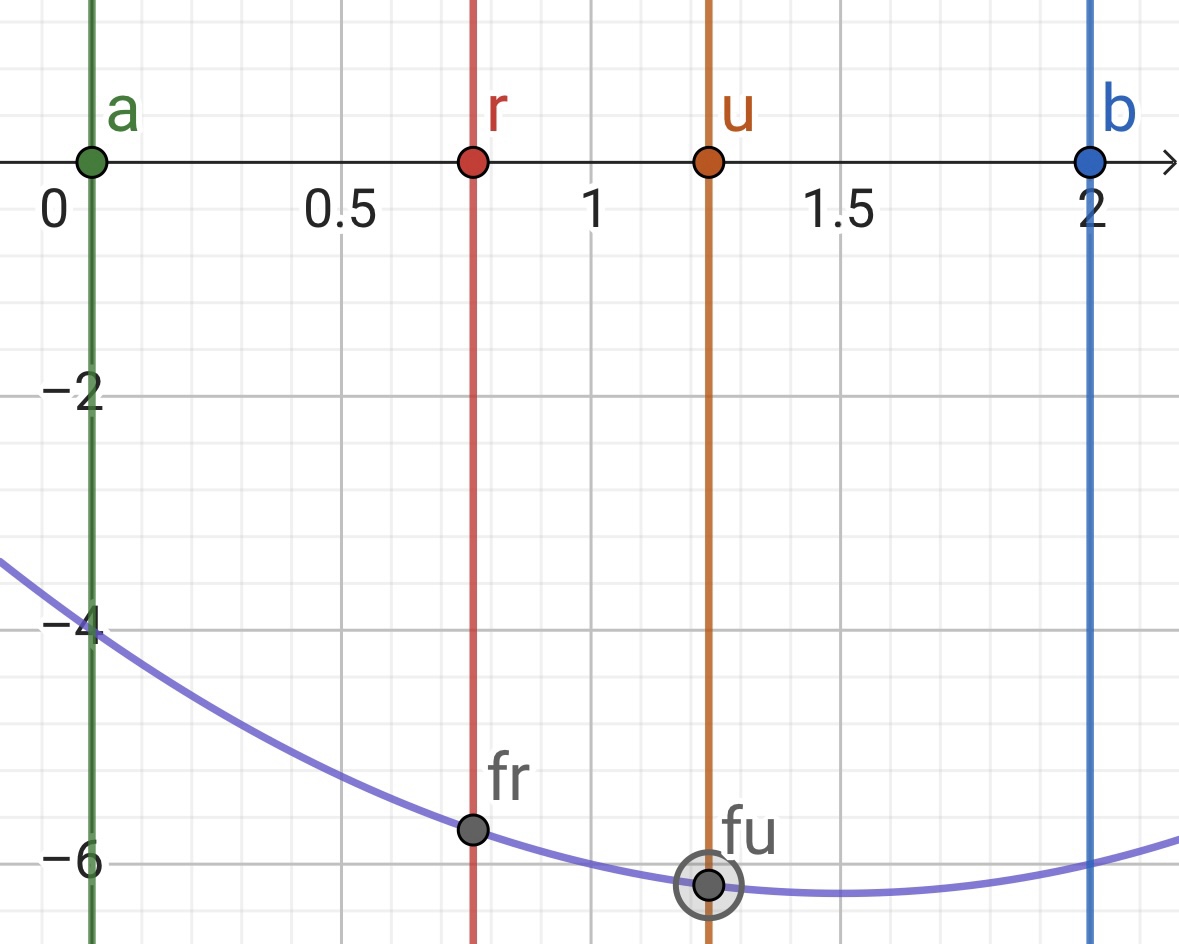
假设函数f在[a,b]上有且仅有一个极小值点p（没有画出），显然f在[a,p]上单减，在[p,b]上单增。

计算f(r)-f(u)，如果大于0，说明r左边是单减的，p一定在r的右边，所以下一次分割的范围变为[r,b]。

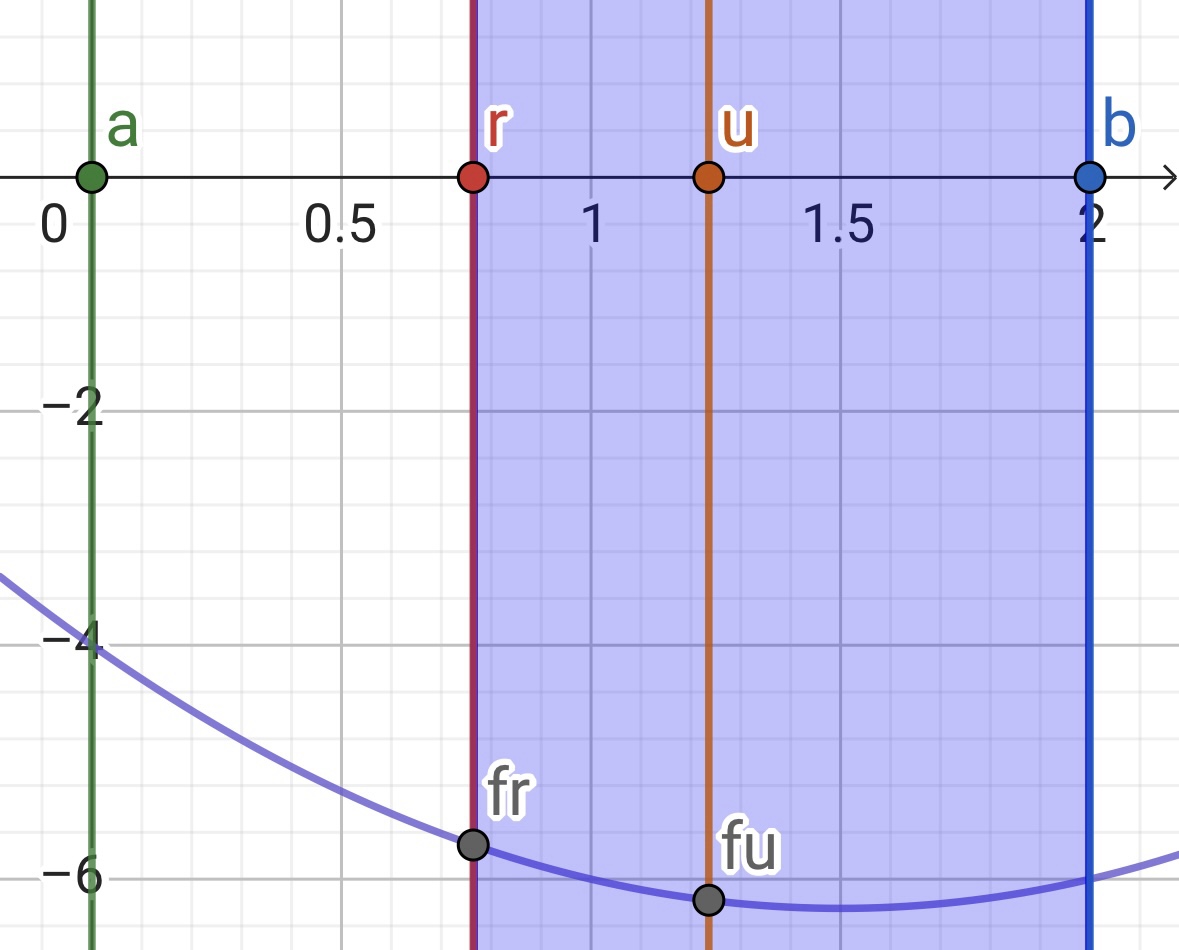
反之，如果小于0，则设置范围为[a,u]，如下图

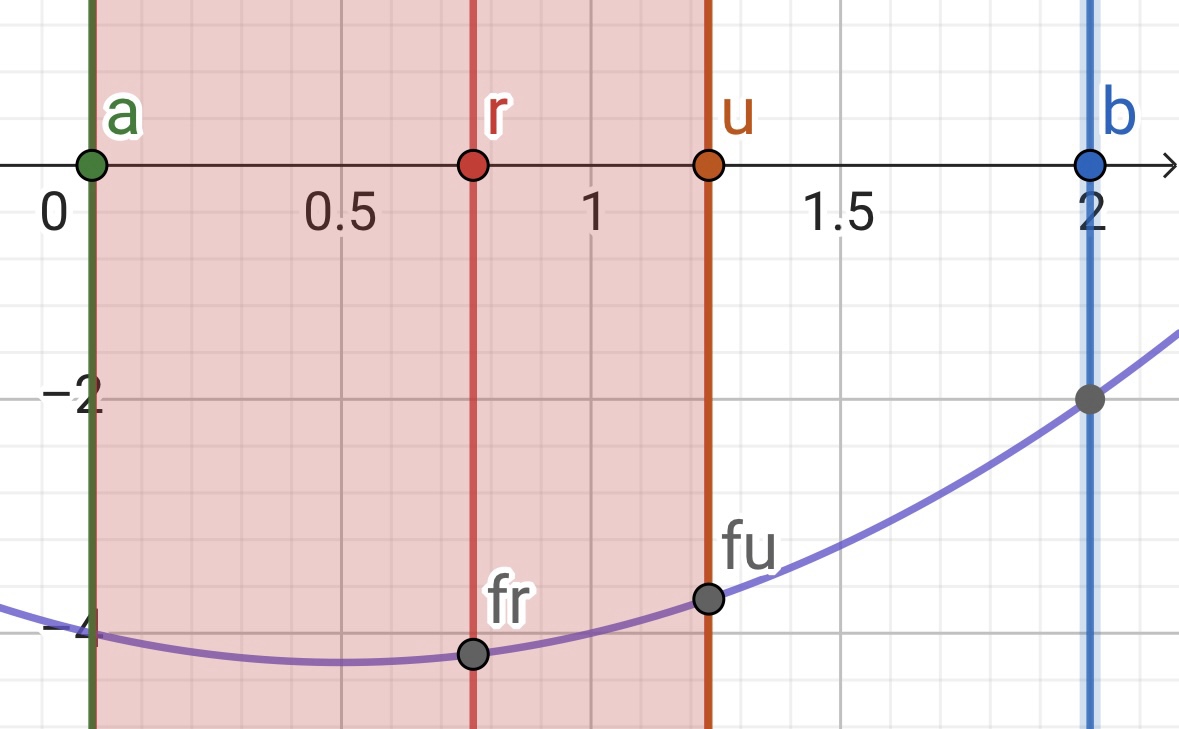
这里需要注意，[r,u]的单调性不能判断，因为如果p在[r,u]内，那f(r)和f(u)的大小就不能反映[r,u]内的单调性。当然不管范围取哪边都会覆盖到[r,u]。

之后就是一直重复上述步骤，来缩小范围逼近p点，终止条件就是u和r的距离小于精确度0.001。

一些可能出现的情况，如果范围内没有极值点，最后会逼近到最值点。但是在这里不考虑这个问题。

代码讲解

首先先展示我最开始写的老师说逻辑混乱matlab代码。

function [x,fx]=test(a,b)
    [r,u]=f2(a,b);
    [x,fx]=f3(a,b,r,u);
end

function y = f(x)
    y = x*x-3*x-4;
end

function [r,u]=f2(a,b)
    r=a+0.382*(b-a);
    u=a+0.618*(b-a);
end

function [x,fx]=f3(a,b,r,u)
    if f(r)>f(u)
        [x,fx]=f4(a,b,r,u);
    else
        [x,fx]=f5(a,b,r,u);
    end
end

function [x,fx]=f4(a,b,r,u)
    if u-r<0.001
        x=u;
        fx=f(u);
        fprintf('x*=%f,f*=%f',x,fx);
        return;
    end
    a=r;
    [r,u]=f2(a,b);
    [x,fx]=f3(a,b,r,u);
end

function [x,fx]=f5(a,b,r,u)
    if u-r<0.001
        x=r;
        fx=f(r);
        fprintf('x*=%f,f*=%f',x,fx);
        return;
    end
    b=u;
    [r,u]=f2(a,b);
    [x,fx]=f3(a,b,r,u);
end

可以看出我严格按照题目要求，把每一个步骤都用函数表示出来了，对照上面的题目描述应该可以很清晰的看懂，就不过多解释了。

但是这样写有太多多余的和重复的函数了，其实可以不用写得这么麻烦。由于我用得最顺手的还是C++，所以之后的代码用C++写。

首先是对我原本代码优化过的递归写法的版本，

#include<iostream>
#include<tuple>
using namespace std;

#define eps 0.001

double f(double x){
    return x*x-3*x-4;
}

tuple<double,double> f3(double a,double b){
    double r,u,fr,fu;
    r=a+0.382*(b-a);
    u=a+0.618*(b-a);
    fr=f(r);fu=f(u);
    if(u-r<eps)
        return (fr>fu)?tuple{u,fu}:tuple{r,fr};
    else
        return (fr>fu)?f3(r,b):f3(a,u);
}
int main(){
    double a,b;
    cin>>a>>b;
    auto [x,fx]=f3(a,b);
    cout<<x<<" "<<fx<<endl;
    return 0;
}

这个代码看起来就很简单，f3的作用就是在[a,b]内查找极小值点。它的步骤如下：

计算分割r和u的值，还有它们的函数值fr和fu。
如果r和u的距离小于eps，那么就返回一个二元组，包括r和u中最接近极小值点的一个，以及它的函数值。
比较fr和fu的大小，并缩小范围并继续搜索，大于的话在[r,b]查找，小于的话在[a,u]查找。

从原本题目的5步描述变成了3步。

当然这个代码也不一定需要递归来写，一般情况下迭代的方法都会优于递归，而且可以看出这是个尾递归，尾递归可以很轻易的写成迭代形式，下面是迭代的写法

#include<iostream>
#include<tuple>
using namespace std;

#define eps 0.001

double f(double x){
    return x*x-3*x-4;
}

tuple<double,double> f3(double a,double b){
    double r,u,fr,fu;
    r=a+0.382*(b-a);
    u=a+0.618*(b-a);
    fr=f(r);fu=f(u);
    while(!(u-r<eps)){
        if(fr>fu)
            a=r;
        else
            b=u;
        r=a+0.382*(b-a);
        u=a+0.618*(b-a);
        fr=f(r);
        fu=f(u);
    }
    return (fr>fu)?tuple{u,fu}:tuple{r,fr};
}
int main(){
    double a,b;
    cin>>a>>b;
    auto [x,fx]=f3(a,b);
    cout<<x<<" "<<fx<<endl;
    return 0;
}

迭代的思路和递归差不多，迭代也是在每次循环时缩小范围。

简单的时间复杂度分析，可以看到范围每次缩小到原来的0.618，可以很轻易的算出这个算法需要计算$\lceil log_{0.618}(\frac{eps}{0.236(b-a)})\rceil$次。显然，这个算法的时间复杂度是对数级的，随着范围的增大，计算次数的增长很慢。

通用化改进

可以看出之前写的f3遍写出来之后，只能对应求解一个函数f的极小值点，而且分割的方式也固定了，我们可以通过下面的改进使这个函数更加通用更加灵活。

将函数f作为一个参数，接受一个double返回一个double的函数，传入f3。
将u-r<eps改为传入一个接受两个double（即范围区间）返回一个bool的函数，这样可以更加灵活的调整精确度，和设置终止条件。
传入fr和fu的比较函数，这样可以通过设置大于或者小于来求极小值或极大值，或者别的更加神奇的用法。
像我最开始写的那样，用一个函数f2来计算分割区间[r,u]，即传入一个函数f2，接受两个double返回两个double，这样可以更加灵活的用不同分割方式。

由于参数太多，如果要写成单个函数的话函数声明会很长很不好看，而且使用起来设置参数很不方便，所以我把它包装成了一个函数对象。

#include<iostream>
#include<tuple>
#include<functional>
using namespace std;

struct PSearch{
    function<bool (double,double)>
    cond;
    
    function<bool (double,double)>
    cmp;
    
    function<tuple<double,double> (double,double)>
    section;

    tuple<double,double>
    operator()(function<double (double)>f,double a,double b){
        double r,u;
        double fr,fu;
        tie(r,u)=section(a,b);
        fr=f(r);fu=f(u);
        while(!cond(r,u)){
            if(cmp(fr,fu))
                a=r;
            else
                b=u;
            tie(r,u)=section(a,b);
            fr=f(r);
            fu=f(u);
        }
        return cmp(fr,fu)?tuple{u,fu}:tuple{r,fr};
    }
};

int main(){
    PSearch F;

    F.cond=[](double r,double u){
        return u-r<0.001;
    };

    F.cmp=less<double>();

    F.section=[](double a,double b){
        double r=a+0.382*(b-a);
        double u=a+0.618*(b-a);
        return tuple{r,u};
    };

    auto [x2,f2]=F([](double x){return x*x-3*x-4;},-1,1);
    cout<<x2<<" "<<f2<<endl;
    return 0;
}

虽然把每个参数都单独分离为了成员变量，但是类型名还是太长了，所以我尽量把类型名和变量名换行写，以免类型名太长把变量名顶到右边，影响阅读。

函数对象我起名叫PSearch(P-Search)，就是查找P点的意思。解释一下每个参数的作用，

cond是终止条件函数，判断区间[r,u]是否终止，一般情况下就是u-r<eps。
cmp是函数值的比较函数，如果是大于的话求的是极小值，小于求的是极大值。可能也可以有更加神奇的用法。
section是区间分割函数，接受区间[a,b]，返回分割后的[r,u]。结合cond，也可以是不收缩而是扩张，但是还没想出扩张有什么用。
重载了括号运算符，可以把结构体当函数使用（也叫函数对象），接受一个函数f和区间[a,b]，返回极值点和极值。

使用方法，首先创建一个PSearch函数对象F，然后设置终止条件、比较函数、分割函数，之后将待求极值点的函数和查询区间传入F，就可以求出极值点和极值。

模板化改进

重新思考一下这个问题，我们求的是函数的极值点，重点是函数。上面的代码中我们的函数对象已经可以求一个输入为double，输出为double的函数的极值点了。但是这是C++，我们可以使用模板，来让这个函数对象更加通用。

首先不难看出我们需要关心的只有两个类型，即待求函数的参数类型（以下简称PT，parament type）和返回值类型（以下简称RT，result type）。在前面的问题中，这两种类型均为浮点型double，现在重新看看前面的代码，将里面的double全部替换为PT和RT。

首先明确，涉及到范围的类型都是PT，这些包括a，b，r，u。涉及到函数值的类型都为RT，这些包括fr，fu和查找出的极值。

cond，终止条件，参数为r和u，所以两个参数的类型都为PT。

cmp，比较函数，参数为fr和fu，所以两个参数的类型都为RT。

section，分割函数，参数为a和b，返回r和u，所以四个参数的类型都为PT。

重载括号运算符，返回值为一个二元组，包含极值点和极值，所以返回值类型为tplue<PT,RT>第一个参数为函数f，接受PT返回RT，所以类型为function<RT (PT)>。后面两个参数a和b类型为PT。

由于使用了模板，所以我把PSearch单独写到了一个头文件里面使用。

#ifndef PSEARCH_H
#define PSEARCH_H

#include<tuple>
#include<functional>

template<typename PT,typename RT>
struct PSearch{
    std::function<bool (PT,PT)>
    cond;
    
    std::function<bool (RT,RT)>
    cmp;
    
    std::function<std::tuple<PT,PT> (PT,PT)>
    section;

    std::tuple<PT,RT>
    operator()(std::function<RT (PT)>f,PT a,PT b){
        PT r,u;
        RT fr,fu;
        std::tie(r,u)=section(a,b);
        fr=f(r);fu=f(u);
        while(!cond(r,u)){
            if(cmp(fr,fu))
                a=r;
            else
                b=u;
            std::tie(r,u)=section(a,b);
            fr=f(r);fu=f(u);
        }
        return cmp(fr,fu)?std::tuple{u,fu}:std::tuple{r,fr};
    }
};

#endif

之后在代码中引入PSearch，来使用

#include<iostream>
#include"PSearch.h"
using namespace std;
int main(){
    PSearch<double,double>F;

    F.cond=[](double r,double u){
        return u-r<0.001;
    };

    F.cmp=less<double>();

    F.section=[](double a,double b){
        double r=a+0.382*(b-a);
        double u=a+0.618*(b-a);
        return tuple{r,u};
    };

    auto [x2,f2]=F([](double x){return x*x-3*x-4;},-1,1);
    cout<<x2<<" "<<f2<<endl;
    return 0;
}

在创建函数对象时指定参数类型和返回值类型，然后用法同之前一样。

总结

至此，我们已经可以说把三分法求极值点的问题彻底弄透了，其实主要就是迭代缩小范围，逼近极值点，后面的代码也只是前段时间太忙了，太久没写代码了，用来练练手。