线性方程组求解（C++版）

同样是matlab实验课上的一个问题，用matlab分类讨论并求线性方程组的基础解系和特解，当时上课我写得不好其实我高代51分，连基础解系是什么都不知道，所以用C++重新写一遍，顺便学习一下高代

线性方程组的一些知识

首先我们先来了解线性方程组的一些知识，我认为需要用到的就是下面这些。

1. 线性方程组的一般形式
2. 线性方程组的矩阵形式
3. 消元法化为行阶梯矩阵
4. 求矩阵的秩
5. 线性方程组有解判别定理
6. 线性方程组解的结构

这里只说怎么样求解，至于为什么这样能够求解，我也不知道。我不配说我是学数学的

线性方程组的一般形式

以下是一个包含 $m$ 个方程、$n$ 个未知变量的线性方程组的一般形式：

$$\begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \vdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n = b_m \end{cases}$$

其中，$a_{ij}$（$i = 1, 2, \ldots, m$；$j = 1, 2, \ldots, n$）是方程组的系数，$b_i$（$i = 1, 2, \ldots, m$）是方程组的常数项，$x_j$（$j = 1, 2, \ldots, n$）是未知变量。

线性方程组的矩阵形式

线性方程组也可以写成矩阵和向量相乘的形式

$$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix}$$

$A$为系数矩阵，是一个$m\times n$的矩阵：

$$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}$$

$x$为包含n个未知变量的列向量：

$$x = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}$$

$b$为包含n个常数项的列向量：

$$b = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}$$

也可以写成这样：

$$Ax=b$$

消元法化为行阶梯矩阵

消元法主要就是利用初等行变换，将矩阵化简为行阶梯矩阵，主要就是下面三种变换

1. 用一非零的数乘某一行
2. 把一行的倍数加到另一行
3. 互换两行的位置

目的就是尽量把对角线上的元素全部化为1，便于计算，因为写起来太麻烦了，这里不演示过程了，大家可以随便找本高代教材看看例题。

求矩阵的秩

矩阵的秩是矩阵中行向量或列向量的极大线性无关组中的向量个数。

行阶梯形矩阵的秩很容易判断，就是非0行的数量。

线性方程组有解判别定理

线性方程组有解的充要条件是它的系数矩阵和增广矩阵的秩相等。

如果秩等于未知数的个数则有唯一解，否则有无穷解。

线性方程组解的结构

在解不唯一的情况下，

齐次线性方程组的任一解可以由基础解系线性表出。

非齐次线性方程组的解由基础解系和一个特解构成。

这里我偷个懒，贴个我在知乎看见的，文章，按照这篇文章说的方法求基础解系。

特解的话，增广矩阵化为行最简矩阵，提取非零行和主元列，构成新的增广矩阵，可以发现系数矩阵变成了一个单位矩阵，常数项列向量就为主元变量的一个特解，自由变量为0。

C++的一些准备工作

首先确定一下我们求解的过程，

1. 求出系数矩阵和增广矩阵的秩，判断是无解还是唯一解还是无穷解。
2. 唯一解的话增广矩阵化为行最简矩阵，右边常数项的列向量就是解向量。
3. 求基础解系的话，系数矩阵化为行最简矩阵，然后扩成方阵，用单位阵减去这个方阵，然后提取自由变量所在的列向量，构成基础解系。
4. 求无穷解的一个特解，增广矩阵化为行最简矩阵，按系数矩阵补成方阵，提取常数项列向量就是一个特解

这里面需要用到的并且需要我们自己实现的操作有：

1. 矩阵操作（C++不自带矩阵，所以要自己实现）
2. 矩阵拼接（用于求增广矩阵）
3. 化为行最简矩阵并且求秩（用处很多不解释）
4. 矩阵按列提取（用于提取解向量和基础解系）

所以接下来先实现上面的这些功能

矩阵类

C++主要不是用于数学计算的，标准库里面没有矩阵相关的类和函数，我也不会找库，所以先花一点点时间搓个矩阵类。为了通用使用了模板，容器方面权衡了一下还是选择了vector而不是valarray，虽然valarray对计算有优化，但是更多的涉及数组和内存的操作，这方面不如vector，而且矩阵叉乘并不能使用valarray自带的乘法计算，也是要自己实现，所以不如使用更加通用的vector。

先写个简单的矩阵类mat，只重载输入输出和下标运算，还有获取行和列，其他功能后面再补充

template<typename T>
class mat{
    private:
        int n,m;
        std::vector<std::vector<T>>data;
    public:
        mat():n(0),m(0){}
        mat(const int n,const int m):n(n),m(m){
            data=std::vector<std::vector<T>>(n,std::vector<T>(m));
        }
        int row()const{return n;}
        int col()const{return m;}
        std::vector<T>& operator[](int i){
            return data[i];
        }
        const std::vector<T>& operator[](int i)const{
            return data[i];
        }
        friend std::istream& operator>>(std::istream& in,mat&A){
            for(auto&row:A.data){
                std::copy_n(std::istream_iterator<T>(in),row.size(),row.begin());
            }
            return in;
        }
        friend std::ostream& operator<<(std::ostream& out,const mat&A){
            for(auto&row:A.data){
                std::copy(row.begin(),row.end(),std::ostream_iterator<T>(out," "));
                out<<"\n";
            }
            return out;
        }
};

矩阵拼接

这里单独实现一个函数combine，用于将两个行数相等的矩阵拼接为一个新的矩阵，参数为两个矩阵，返回一个矩阵。

template<typename T>
mat<T> combine(const mat<T>&A,const mat<T>&B){
    int n=A.row();
    int m=A.col()+B.col();
    mat<T>C(n,m);
    for(int i=0;i!=n;++i){
        copy(B[i].begin(),B[i].end(),
        copy(A[i].begin(),A[i].end(),C[i].begin()));
    }
    return C;
}

化为行最简矩阵和求秩

这里需要实现初等行变换，因为行向量使用的是vector，所以需要我们手动重载vector的加减乘除：

template<typename T>
std::vector<T> operator-(const std::vector<T>&a){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),c.begin(),std::negate<T>());
    return c;
}

template<typename T>
std::vector<T> operator+(const std::vector<T>&a,const std::vector<T>&b){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),b.begin(),c.begin(),std::plus<T>());
    return c;
}

template<typename T>
std::vector<T> operator-(const std::vector<T>&a,const std::vector<T>&b){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),b.begin(),c.begin(),std::minus<T>());
    return c;
}

template<typename T>
std::vector<T> operator*(const T&k,const std::vector<T>&a){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),c.begin(),[&k](const T&a){return k*a;});
    return c;
}

template<typename T>
std::vector<T> operator/(const T&k,const std::vector<T>&a){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),c.begin(),[&k](const T&a){return k/a;});
    return c;
}

template<typename T>
std::vector<T> operator*(const std::vector<T>&a,const T&k){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),c.begin(),[&k](const T&a){return a*k;});
    return c;
}

template<typename T>
std::vector<T> operator/(const std::vector<T>&a,const T&k){
    std::vector<T>c(a.size());
    std::transform(a.begin(),a.end(),c.begin(),[&k](const T&a){return a/k;});
    return c;
}

template<typename T>
std::vector<T>&operator+=(std::vector<T>&a,const std::vector<T>&b){
    return a=a+b;
}

template<typename T>
std::vector<T>&operator-=(std::vector<T>&a,const std::vector<T>&b){
    return a=a-b;
}

template<typename T>
std::vector<T>&operator/=(std::vector<T>&A,const T&k){
    std::for_each(A.begin(),A.end(),[&k](T&a){a/=k;});
    return A;
}

然后就是用初等行变换化为行最简矩阵

mat<T> rref(const mat<T>&A){
	mat<T> B(A);
	int i=0,n=B.col();
	for(auto it=B.data.begin();it!=B.data.end()&&i!=n;it++,i++){
		auto p=find_if(it,B.data.end(),[i](auto&x){return x[i]!=T{};});;
		while(p==B.data.end()){
			if(++i==n)break;
			p=find_if(it,B.data.end(),[i](auto&x){return x[i]!=T{};});
		}
		if(p==B.data.end())break;
		iter_swap(it,p);
		auto&a=*it;
		a/=a[i];
		for_each(B.data.begin(),it,[i,&a](auto&b){if(b[i]==T{})return;b-=(b[i]*a);});
		for_each(it+1,B.data.end(),[i,&a](auto&b){if(b[i]==T{})return;b-=(b[i]*a);});
	}
	return B;
}

求秩的话，我只会数向量，不会计算方法，目前实现就用化为行最简矩阵，数不全为零的向量。

int rank(){
	return n-std::count(data.begin(),data.end(),std::vector<T>(m));
}

矩阵按列提取

可以提取单列或者多列，多列用vector传入，这两个函数作为成员函数实现。

mat<T> getCols(int col){
	mat<T> A(n,1);
	for(int i=0;i!=n;++i)
		A[i][0]=data[i][col];
	return A;
}
mat<T> getCols(std::vector<int> cols){
	mat<T> A(n,cols.size());
	for(int i=0;i!=n;++i)
		for(int j=0;j!=cols.size();++j)
			A[i][j]=data[i][cols[j]];
	return A;
}

其他函数

这些因为我最开始设计的时候不规范，不好归类，所以算作其他函数了。

将行最简矩阵补成方阵，同时主元的行列位置保持一致，这个函数不规范的原因是不知道叫什么名字，以及只能对行最简矩阵使用，其实我最早在设计的时候应该把行最简矩阵作为继承自mat的子类的，总之这个函数暂时只能对行最简矩阵发挥预想的效果。

mat<T> toSquare(const mat<T>&A){
	int n=A.col();
	mat<T> B(n,n);
	for(auto&a:A.data){
		auto it=std::find_if(a.begin(),a.end(),[](const T&a){return a!=T{};});
		if(it==a.end())break;
		int i=it-a.begin();
		std::copy(a.begin(),a.end(),B[i].begin());
	}
	return B;
}

还有一个简单的生成单位矩阵的函数对角矩阵的函数，本来是想做单位矩阵的，但是使用了模板，没办法确定每个类型的乘法单位元，所以改为对角矩阵，手动设置对角线上的元素。

template<typename T>
mat<T> diag(int n,T k){
    mat<T> A(n,n);
    for(int i=0;i!=n;++i)
        A[i][i]=k;
    return A;
}

还有重载了矩阵减法，偷个懒不判断行列数相等了：

template<typename T>
mat<T> operator-(const mat<T>&A,const mat<T>&B){
    mat<T>C(A.row(),A.col());
    std::transform(A.data.begin(),A.data.end(),B.data.begin(),C.data.begin(),std::minus());
    return C;
}

还有删除矩阵的最后一行，会用到这个是因为我之前对增广矩阵化为方阵的处理不好最后会多出一行，所以在化为方阵之后要删掉一行。

void pop_back(){
    data.pop_back();
    --n;
}

C++求解过程

这种方法其实就是我们手动求解线性方程组的通解和特解的方法，只是用编程来模拟手动求解的过程，所以我称之为朴素方法可能它有其他的名字但是我也不知道。

首先把上面那些代码全部塞到一个头文件里面，然后引入#include"mat.h"，因为上面的代码写的太乱了，所以我就不整合出来丢人现眼了，如果我之后把它整得好看了我会再写篇文章。

然后编写求解过程，以下就是主函数的内容，输入输出加入了一点提示，也可以去掉输入输出把它改为一个求解的函数：

int n,m;
    
mat<double>A;
mat<double>b;
mat<double>B;
mat<double>SS;
cout<<"n=";cin>>n;
cout<<"m=";cin>>m;
A=mat<double>(n,m);
b=mat<double>(n,1);
cout<<"A="<<endl;cin>>A;
cout<<"b="<<endl;cin>>b;

auto Ab=combine(A,b);
auto rref_A=rref(A);
auto rref_Ab=rref(Ab);

int rank_A=rref_A.rank();
int rank_Ab=rref_Ab.rank();

if(rank_A==rank_Ab){
    if(rank_A==m){
        cout<<"有唯一解"<<endl;
        auto SS=rref_Ab.getCols(m);
        auto B=SS;
    }
    else{
        cout<<"有无穷解"<<endl;
        auto Sq=toSquare(rref_Ab);
        Sq.pop_back();
        SS=Sq.getCols(m);
        Sq=diag(m,1.0)-toSquare(rref_A);
        vector<int> freeCols;
        for(int i=0;i!=m;++i){
            if(abs(Sq[i][i]-1.0)<=1e-6)
                freeCols.emplace_back(i);
        }
        B=Sq.getCols(freeCols);
    }
}
else{
    cout<<"无解"<<endl;
    B=mat<double>();
    SS=mat<double>();
}
cout<<"B=\n"<<B<<endl;
cout<<"SS=\n"<<SS<<endl;

测试

之后就是测试了，已知matlab上用A\b，即A的伪逆乘b的话，在某些奇异矩阵的情况下会有问题，例如对于

$$A = \begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix} , b=\begin{pmatrix} 3 \\ 6 \end{pmatrix}$$

以下分别是我在matlab和我自己写的程序上的测试结果，

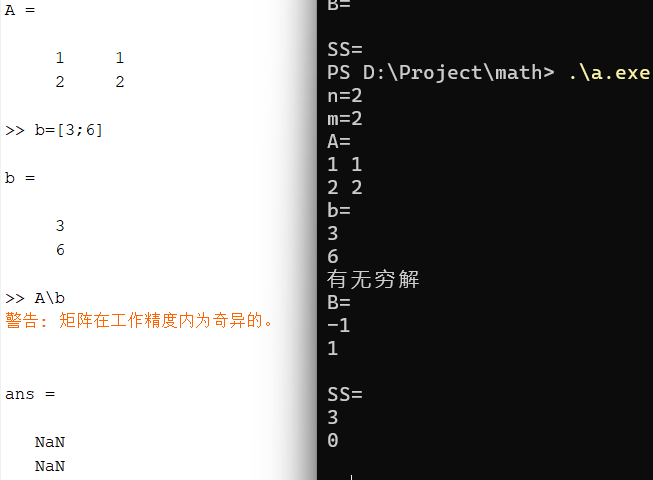
显然对于这组数据matlab并不能求出正确结果，根据上网搜索这是因为matlab使用最小二乘法求的，具体我也不懂。朴素方法求出的特解带入验证显然正确。