一个博客

随便写写

0%

编译期打表

发表于 更新于 分类于

本文介绍一种实用的骗分技巧，众所周知最好的算法就是时间复杂度就是$O(1)$的算法，打表法，借助C++的编译期计算和一点点的模板知识，我们可以实现在编译期打表，大大减少运行时间。

使用场景

实际中能使用编译期打表的场景其实很少，而且编译期打表的限制很多。首先明确为什么要打表，打表的目的是为了简化复杂计算，是一种空间换时间的策略。它的缺点也很多

  1. 受到编译器和编译参数影响，这个主要是递归深度和迭代次数的限制，以及低版本的C++可能不支持constexpr。
  2. 内存限制，因为题目有内存限制，打表会使用大量内存，有些编译的时候能够通过不会爆内存，但是可能运行时在某些情况下还是会爆内存，所以要预留足够的运行内存。
  3. 输入限制，打表法本质上只是做映射，基本只能应付简单的输入和输出，以及输入少的情况，如果有大量复杂输入和输出不建议使用打表法，一般这种情况下使用打表会比题目本身还要困难。

所以打表法不是必须的，只是一种类似于投机取巧的方法，不会影响也不大。下面来看看编译期打表如何操作。

编译期计算

C++哪个版本加入的编译期计算不记得了，主要就是使用constexpr修饰的函数可以在编译期调用，如果参数能够在编译期求值，并且函数不依赖其他运行时变量，那这个函数就可以在编译期调用。

其实这个关键字还有一个更加极端的版本consteval，只能在编译期计算，但是这个关键字比较新，比赛环境不一定能用，所以尽量不要使用。

使用vs code或者其他有静态分析的IDE的时候，尝试下面代码，鼠标移动到等号上应该可以看到，

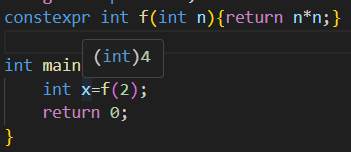
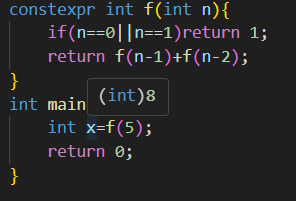
没有运行就直接求出值了，这是编译期求值的比较直观的表现。上面这个函数太简单了，来个简单的编译期递归也是可以的，

编译期结果的保存（现代版）

因为编译期不能动态分配内存，所以很多容器都不能使用，C风格的数组也不能使用，这种情况下怎么保存计算的结果就成了问题，现在可以在编译期中使用array这个容器，这就使得编译期打表变得非常简单了，首先展示一下基本形式

1
2
3
4
5
constexpr auto A=[]{
    array<int,10>res{};
    //计算代码
    return res;
}();

就这么简单，可以用鼠标放在A上试一下，

也可以使用for和调用其他constexpr的函数，

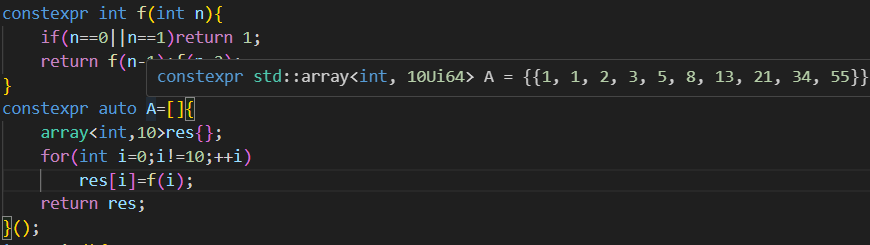
非常的简单就是套格式就行了，

编译期结果的保存（原始版）

上面的方法比较现代，在能够在编译期使用array之前，原始的人类使用的是模板递归来保存数据，形式大概如下，

1
2
3
4
5
6
7
8
9
template<int N>
struct Table{
    Table<N-1>pre;
    int val=N;
};
template<>
struct Table<0>{
    int val=0;
};

要理解这个东西需要一些模板递归的知识，这个结构体最后会保存成一个神奇的样子，可能像这样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Table<N>{
  Table<N-1>{
    Table<N-2>{
      //一些代码
      Table<0>{
        int val;
      }
      //一些代码
      int val
    }
    int val;
  }
  int val;
}

这些数据如何排列的，以及如何读取，需要对C语言结构体有些了解。首先这些数据就是按照0到N的顺序，连续排列的N+1个int。如何读取呢，使用C语言指针的方式读取，可以试着下面的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<iostream>
using namespace std;
template<int N>
struct Table{
    Table<N-1>pre;
    int val=N;
};
template<>
struct Table<0>{
    int val=0;
};
Table<10>A;
int main(){
    int *p=(int*)&A;
    for(int i=0;i!=10;++i)
        cout<<*(p+i)<<endl;
    //也可以使用copy的方式
    //copy_n(p,10,ostream_iterator<int>(cout," ");
    return 0;
}

不过这种方法使用起来太麻烦了，不建议使用。接下来进行一些实战，因为我现在用leetcode所以用leetcode演示。

简单的实战

爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

  1. 1 阶 + 1 阶
  2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

  1. 1 阶 + 1 阶 + 1 阶
  2. 1 阶 + 2 阶
  3. 2 阶 + 1 阶

提示：

$1 <= n <= 45$

显然这是一道动规题，状态转移方程为dp[i]=dp[i-1]+dp[i-2];，数据范围只有46个（包含0）。非常的常规，直接算其实也不麻烦，下面是打表的写法

1
2
3
4
5
6
7
8
9
10
11
12
constexpr auto A=[]{
    array<int,46>res{0,1,2};
    for(int i=3;i!=46;++i)
        res[i]=res[i-1]+res[i-2];
    return res;
}();
class Solution {
public:
    int climbStairs(int n) {
        return A[n];
    }
};

打表建议打在全局变量，局部变量可能会爆内存。非常的简单直接返回结果就行了。

使用辅助函数的实战

阶乘后的零

这题也是动规，但是应该有不是动规的写法，范围是$10^4$，显然可以全打了，能暴力打表就不要动脑子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
constexpr int get5(int N){
    return (N%5!=0)?0:(1+get5(N/5));
}
const int N=1e4;
constexpr auto A=[]{
    array<int,N+1>res{};
    for(int i=1;i<=N;++i)
        res[i]=res[i-1]+get5(i);
    return res;
}();
class Solution {
public:
    int trailingZeroes(int n) {
        return A[n];
    }
};

需要一些处理的实战

x的平方根

不能使用内置函数，而且我脑子不好不会写二分法和牛顿迭代法怎么办呢，打表！看一眼范围$2^{31}-1$，不能暴力打表每个数的平方根。

但是反过来想，可以打表每个数的平方，然后通过查找平方来获取下标就是平方根，这样只需要打$2^{16}$的表

1
2
3
4
5
6
7
8
9
10
11
12
13
const int N=1<<16;
const auto A=[]{
    array<unsigned int,N>res{};
    for(unsigned int i=1;i!=N;++i)
        res[i]=i*i;
    return res;
}();
class Solution {
public:
    int mySqrt(unsigned int x) {
        return upper_bound(A.begin(),A.end(),x)-A.begin()-1;
    }
};

部分打表的实战

位1的个数

多次调用的优化方法，那当然是打表啊！看一眼范围$2^{31}-1$，不能暴力打表。观察到2的32次方就是有32个位，可以只打16位的表，然后取高16位和低16位的1的个数和。

1
2
3
4
5
6
7
8
9
10
11
12
13
constexpr int N=1<<16;
constexpr auto A=[]{
    array<char,N>res{};
    for(int i=1;i!=N;++i)
        res[i]=res[i>>1]+i%2;
    return res;
}();
class Solution {
public:
    int hammingWeight(int n) {
        return A[n>>16]+A[n&0xffff];
    }
};

复杂的实战

全排列

为什么全排列也要打表呢，我也不知道，单纯只是因为它的范围只有6，这种情况就是打表会比较复杂，但是我觉得不打表也复杂。

这里我使用了原始的模板递归来保存全排列的索引，因为array需要固定每个元素的大小，而且编译期没有地址，所以不能用array嵌套来保存每个数字的情况下的全排列。

F是打表的阶乘数。
Table是打表的全排列索引。
pos是打表的偏移量，用于从Table中获取对应N的全排列。
array2vector是将索引映射为题目要求的元素，同时返回vector。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
constexpr auto F=[]{
    array<int,7>res{0,1};
    for(int i=2;i!=7;++i)
        res[i]=i*res[i-1];
    return res;
}();
template<int N>
struct Table{
    Table<N-1>DATA{};
    array<array<int,N>,F[N]>CUR{};
    Table(){
        auto&PRE=DATA.CUR;
        for(int i=0;i!=N;++i){
            for(int j=0;j!=F[N-1];++j){
                for(int k=0;k!=i;++k)CUR[i*F[N-1]+j][k]=PRE[j][k];
                CUR[i*F[N-1]+j][i]=N-1;
                for(int k=i;k!=N-1;++k)CUR[i*F[N-1]+j][k+1]=PRE[j][k];
            }
        }
    }
};
template<>
struct Table<1>{
    array<array<int,1>,1>CUR{{0}};
};
const Table<6>table;
const auto pos=[]{
    array<int,7>res{};
    for(int i=2;i!=7;++i)
        res[i]=res[i-1]+(i-1)*F[i-1];
    return res;
}();
vector<vector<int>>array2vector(vector<int>v){
    int n=v.size();
    int m=F[v.size()];
    int*A=((int*)(&table))+pos[n];
    vector<vector<int>>res(m,vector<int>(n));
    for(int i=0;i!=m;++i)
        for(int j=0;j!=n;++j)
            res[i][j]=v[*A++];
    return res;
}
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        return array2vector(nums);
    }
};

总结

打表不是什么有思想的东西，这是一种实战的暴力解题技巧，是一种经验，所以要在实践中学习怎么使用，高级的还有分段打表，但是我一时间没找到合适的题。