动态规划是一种很基本的思想,用一句话来说就是,用数组将计算中重复计算的数据保存下来,也叫记忆化搜索。
斐波那契数列
举一个经典又简单的例子,斐波那契数列。前两项为1,后面每一项为前面两项之和,按照这个定义可以很轻易的写成递归形式1
2
3
4int fib(int n){
if(n==1||n==2)return 1;
return fib(n-1)+fib(n-2);
}
画出计算的过程可以发现它每一层的右子树都进行了很多次的重复计算。
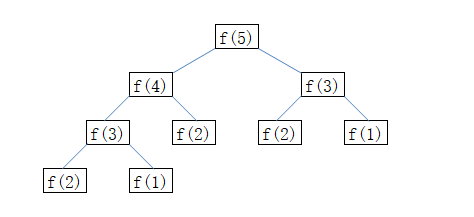
我们可以通过创建一个数组来保存计算过的项,如果需要的项被计算过那就直接使用数组的数据1
2
3
4
5int fib(int n){
static array<int,100>A{0,1,1};
if(A[n])return A[n];
return A[n]=fib(n-1)+fib(n-2);
}
也可以写成迭代的形式,如果我们需要第n项,因为存在依赖关系,那就需要依次计算出前n项1
2
3array<int,100>A{0,1,1};
for(int i=3;i<=n;++i)
A[i]=A[i-1]+A[i-2];
这样就可以在线性时间内得到1到n项斐波那契数列的表
滚动数组优化
但是有时候如果我们只需要一项,而不需要其他项,或者说不能保存每一项的时候,我们可以使用滚动数组优化。
继续看斐波那契数列的例子,后一项仅依赖前两项,并且后面肯定不会用到更加前面的项,所以我们可以只用一个大小为2的数组来计算斐波那契数列1
2
3
4
5
6int fib(int n){
array<int,2>A{1,1};
for(int i=3;i<=n;++i)
A[i%2]+=A[(i-1)%2];
return A[n%2];
}
这个的关键就是用取余来模拟滚动,我画了个图来表现一下滚动(不会做动图,将就着看吧)
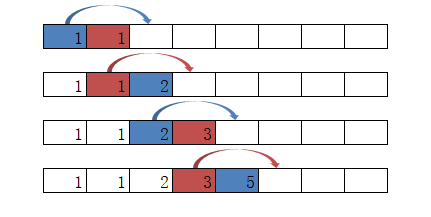
蓝色是奇数项,红色是偶数项,就是这样滚动迭代的。
二维动规
二维和高维的动规其实就是依赖和选择变多了,以及不要忘记动规的名字叫动态规划,尤其是规划,本质上是用算法做出最优选择。
从更好理解的方式来说的话,假设你要以最短的路径从(0,0)走到(x,y),如果有两个位置(a,b)和(c,d)都能走到(x,y),那么最短路径就是走到这两个位置中最近的加上从它们走到目的地的路程,即dp[i][j]=dis[i][j]+min(dp[i-1][j],dp[i][j-1]),这个式子就叫状态转移方程,更高维的动态规划也差不多都是这样,就是要找出前后数据之间存在的依赖关系,分解问题,写出状态转移方程。
这题在leetcode上有一样的题目,最短路径和
非动规题的动规解法
有一些题可能本意不是考动规,而是别的思想,但是数据上可能也存在一些关系,这些题目可能也可以使用动规来写。
leetcode题目:笨阶乘
如果第一眼看不出规律,我们可以把它的前10项列出来1
2
3
4
5
6
7
8
9
10clumsy(1)=1
clumsy(2)=2*1
clumsy(3)=3*2/1
clumsy(4)=4*3/2+1
clumsy(5)=5*4/3+2-1
clumsy(6)=6*5/4+3-2*1
clumsy(7)=7*6/5+4-3*2/1
clumsy(8)=8*7/6+5-4*3/2+1
clumsy(9)=9*8/7+6-5*4/3+2-1
clumsy(10)=10*9/8+7-6*5/4+3-2*1
这样其实还是不容易看出,再调整一下顺序1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16clumsy(1)= 1
clumsy(5)= 5*4/3+2-1
clumsy(9)=9*8/7+6-5*4/3+2-1
clumsy(2)= 2*1
clumsy(6)= 6*5/4+3-2*1
clumsy(10)=10*9/8+7-6*5/4+3-2*1
clumsy(3)= 3*2/1
clumsy(7)= 7*6/5+4-3*2/1
clumsy(11)=11*10/9+8-7*6/5+4-3*2/1
clumsy(4)= 4*3/2+1
clumsy(8)= 8*7/6+5-4*3/2+1
clumsy(12)=12*11/10+9-8*7/6+5-4*3/2+1
现在不难发现,后面几项是相同的,对它们进行上下作差,得到规律就是1
clumsy(n)=n*(n-1)/(n-2)+(n-3)-2*(n-4)*(n-5)/(n-6)+clumsy(n-4)
还能够发现乘除项也是可以通用的,记为f(n)=n*(n-1)/(n-2),现在可以写为1
clumsy(n)=f(n)+(n-3)-2*f(n-4)+clumsy(n-4)
而且我没发现这道题的输入和输出都只是一个数,而且范围不大,于是使用之前说的编译期打表解决1
2
3
4
5
6
7
8
9
10const int N=1e4+1;
constexpr auto A=[]{
array<int,N>M{0,1,2,6,6};
array<int,N>res{0,1,2,6,7};
for(int i=5;i!=N;++i){
M[i]=i*(i-1)/(i-2);
res[i]=M[i]+i-3-2*M[i-4]+res[i-4];
}
return res;
}();
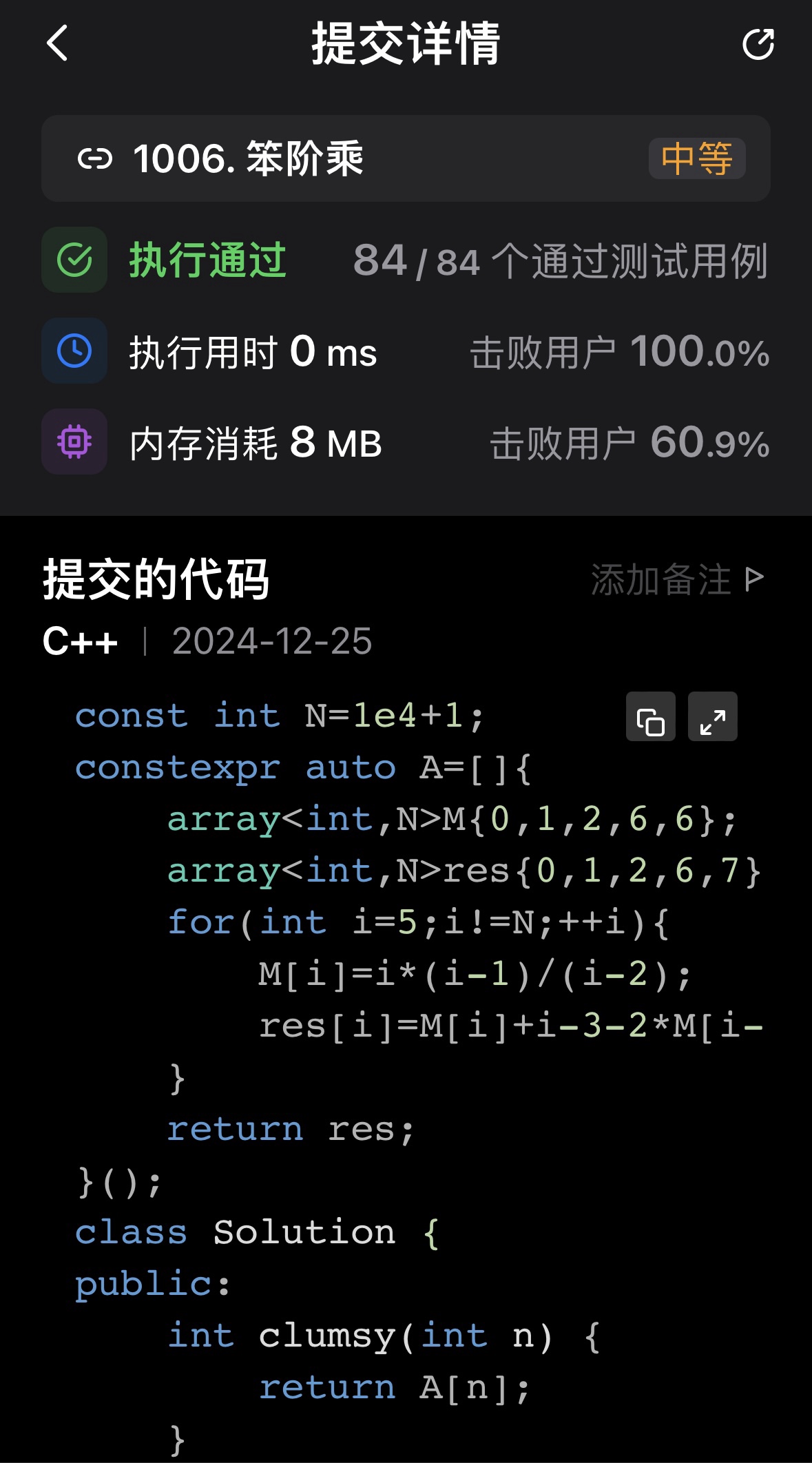
相当完美的案例,下面再说一下滚动数组的写法。
不难发现这个滚动数组的大小为4,用两个大小为4的数组分别保存笨阶乘和乘除项,注意题目是从1开始,所以下标0作为下标4,从第5项开始迭代1
2
3
4
5
6
7
8
9
10int clumsy(int n){
array<int,4>M{6,1,2,6};
array<int,4>A{7,1,2,6};
for(int i=5;i<=n;++i){
A[i%4]+=i-3-2*M[i%4];
M[i%4]=i*(i-1)/(i-2);
A[i%4]+=M[i%4];
}
return A[n%4];
}
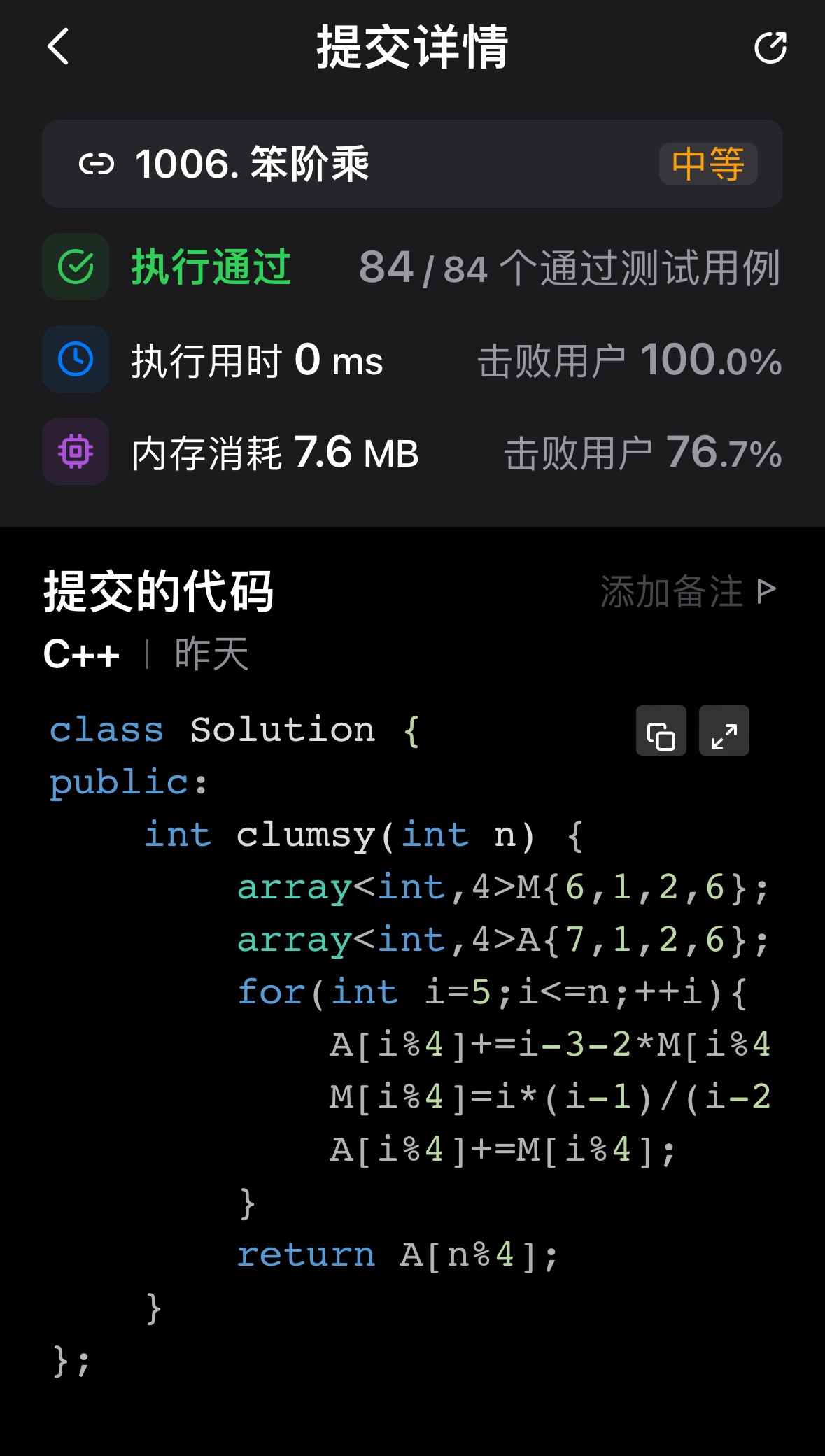
效果也怪好的。
总结
还是那句话,动态规划主要就是要找到重复计算的部分和前后的依赖关系。
其实我这篇文章算是夹带私货了,我就是为了秀一下我用动态规划写了笨阶乘而讲的动态规划。