最近看了一下《具体数学(第二版)》,汉诺塔问题是个非常经典又有趣的问题,写了一些课后习题中的汉诺塔问题的部分,记录一下。
经典汉诺塔问题
先简单说一下什么是汉诺塔问题,有三根柱子和n个大小不一的圆盘,圆盘不能放在比它小的圆盘上。一开始所有的圆盘都在第一根柱子上,我们需要将圆盘移动到第三根柱子上,每次只能从一根柱子移动一个圆盘到另一根柱子上,求最小移动次数。
设三根柱子分别为ABC,以及定义$f(n)$为将n个圆盘从A移动到C需要的步数。现在$f(n)$还是一个抽象的函数,之后来给出它的具体实现。
首先移动0个圆盘肯定是0步,$f(0)=0$。移动一个圆盘需要1步,$f(1)=1$。对于2个圆盘,我们需要先把第一个圆盘移动到B柱上,然后才能把最大的圆盘移动到C柱上,最后再把第一个圆盘放到C柱上。
其实不难发现,要把n个圆盘从一根柱子移到另一根柱子上,需要保证另外两根柱子的最顶上的圆盘都大于要移动的n个圆盘中最大的,因为移动n个圆盘需要用到两根柱子来过渡,如果n=1则没有这个条件。所以记住这个条件,只要满足这个条件我们就可以将n个圆盘移动到任意柱子上
接下来考虑更多圆盘的情况,我们需要把除了最大圆盘以外的n-1个圆盘全部移动到B柱上,解放出最大圆盘并移动到C柱上,之后再把n-1个圆盘移动到C上。汉诺塔是一个很形象的问题,所以我还画了个简单的图片,可以更加直观的看步骤
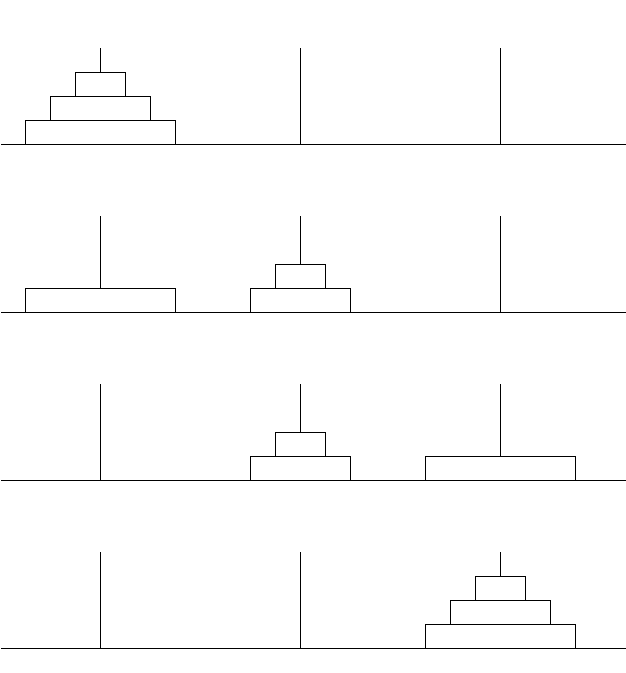
即
所以我认为汉诺塔问题很重要的一个思想就是部分与整体,还有通过定义函数来让步骤更加清晰。
如果是计算机问题,其实到上面就可以结束了,我们已经得到了一个递归的函数来计算步数了,但是这个递归式可以求出通项公式,通过观察
代入先前的n=0和n=1也成立,这样这个问题就算结束了。
相邻移动的汉诺塔问题
课后习题在原问题的基础上加上了一个限制条件。在原问题中圆盘能够在三个柱子之间任意移动,现在圆盘只能在相邻柱子上移动,重新分析一下这个问题。
设$f(n)$为将n个圆盘从A移动到C的步数,显然$f(0)=0$。根据对称性可以知道将n个圆盘从C移动到A也需要$f(n)$步。
所以对于n>0,移动步骤可以描述为
- 将n-1个圆盘从A移动到C
- 将第n个圆盘从A移动到B
- 将n-1个圆盘从C移动到A
- 将第n个圆盘从B移动到C
- 将n-1个圆盘从A移动到C
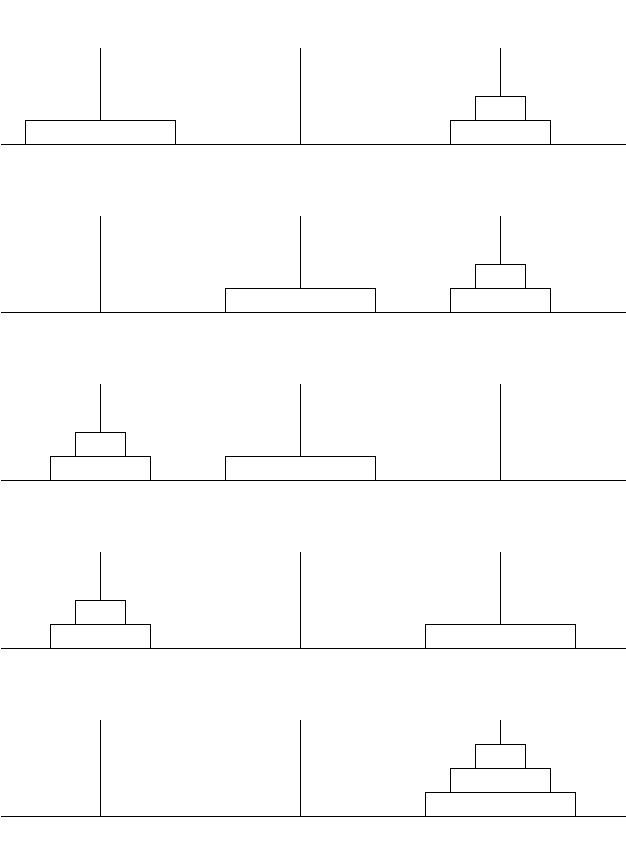
将上述步骤加起来得到$f(n)=3f(n-1)+2$。经过观察得到
对于n=0的情况也成立,所以通项公式为$f(n)=3^n-1$
注意,这里我也不确定是不是最小步数,只能说最小步数一定小于等于这个。
证明每根柱子上都出现过n个圆盘的正确形式
这题的题目其实我不太懂,按照我的理解应该是让我们证明在上题的移动中间过程中A、B、C上都会出现过高度为n的塔。A和C分别在开始和结束的状态为n层塔,所以就是要证明需要先把A上的塔全部移到B上,再把B上的塔全部移到C上。
设$f(n)=f{AB}(n)+f{BC}(n)$,$f{AB}(n)$和$f{BC}(n)$分别为将n个圆盘从A移动到B的步数和从B移到C的步数。显然根据定义,$f{AB}(0)=0,f{BC}(0)=0,f{AB}(1)=1,f{BC}(1)=1$。同样根据对称性,$f{AB}(n)=f{CB}(n),f{BC}(n)=f{BA}(n)$
现在将从A移动n个圆盘(n>0)到C,用经过B的步骤表示
- 将n-1个圆盘从A移动到B
- 将n-1个圆盘从B移动到C
- 将第n个圆盘从A移动到B
- 将n-1个圆盘从C移动到B
- 将n-1个圆盘从B移动到A
- 将第n个圆盘从B移动到C
- 将n-1个圆盘从A移动到B
- 将n-1个圆盘从B移动到C
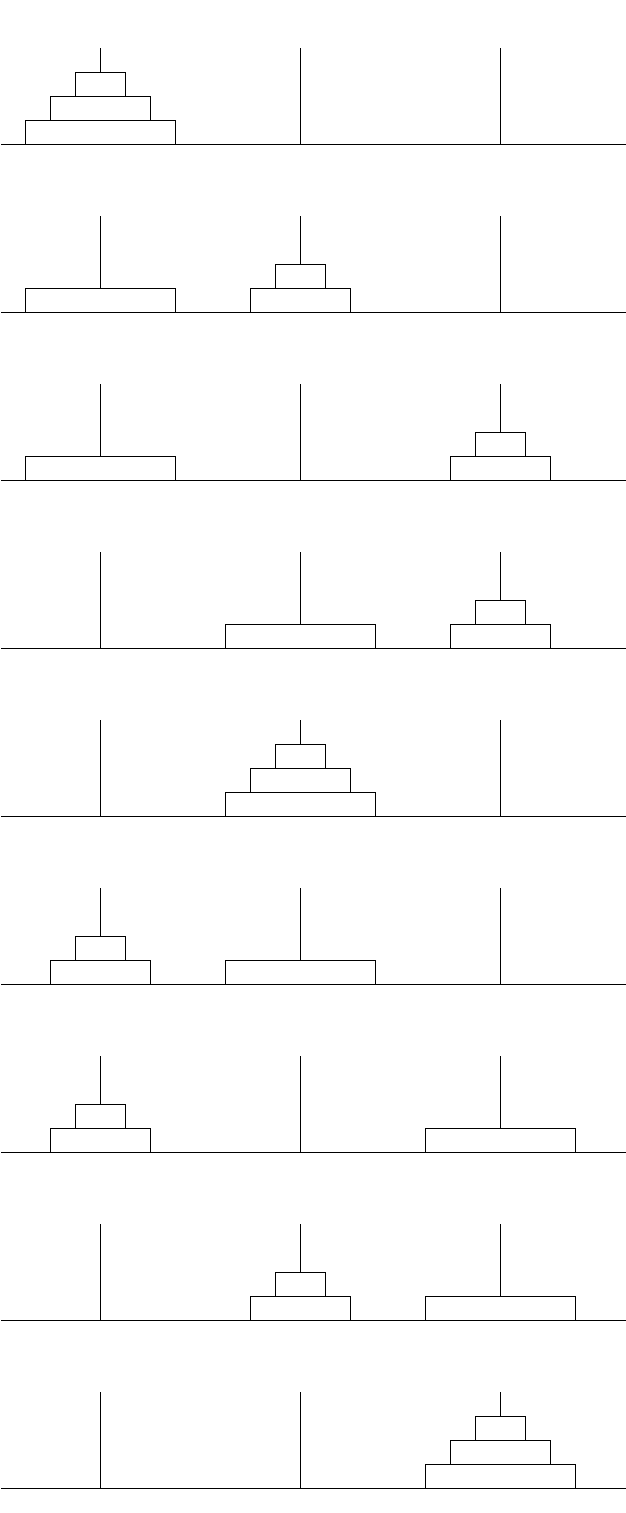
将上面的步骤整理一下得到
代入之前的$f(n)=3f(n-1)+2$,稍微变形一下
还需要讨论一下n=0和n=1的情况。
对于n=0,$f(0)=f{AB}(0)+f{BC}(0)=0$成立
对于n=1,$f(1)=f{AB}(1)+f{BC}(1)=2$成立
所以$\forall n \in N,f(n)=f{AB}(n)+f{BC}(n)$,即从A移动n个圆盘到C,一定会先将n个圆盘移动到B上。
是否存在步数大于$2^n-1$次的合理初始状态
这个也是经典汉诺塔问题的变种,即初始状态不是n个圆盘都在A塔上,看能否找出一种摆放使得将圆盘全部移动到C需要的步数大于$2^n-1$次。
对于这题我还不能够像前面的题一样写出巧妙的数学证明,但是在学数学之前我还是个写代码的,所以我决定先用程序暴搜出结论,再想办法证明,详见下篇文章。