继上篇文章结尾,我用mathematica写了个简陋的可视化图形来展示经典汉诺塔问题的状态关系,这篇文章来把之前的代码写的好看一点。
大概思路
我想的是编写一个函数HNT接受两个参数,S状态空间,即所有合理的圆盘摆放,R柱间移动规则,即允许从哪根柱子移动到哪根柱子,返回边,即状态间的转移关系。
状态的表示同上一篇文章,用三元组表示。因为三根柱子n个圆盘的状态数为$3^n$,手动列出不太现实,所以还是要编写一个函数递归的生成状态空间。
移动规则用二元组表示,即{from,to}的形式,从第一根柱子移动到第二根柱子就是{1,2}。移动规则的数量不多,看题目情况手动输入就行了。
还需要编写两个函数,判断一个状态能否使用这个规则移动,以及获取一个状态在这个规则下移动得到的边。
主要流程就是,对于S中的每一个状态,对于每一个规则,判断能否通过规则集移动,对于可以移动的,应用对应规则获取边。
函数编写
LowBit
状态的表示方法和上篇文章说的一样,所以需要用到lowbit,所以先写一个MMA版的lowbit1
LowBit[x_] := BitAnd[x, -x];
MMA里面的按位且不是&,是一个函数BitAnd。
CanMove
判断可以移动的条件就是比较两根柱子上最小的圆盘的大小,但是需要保证这两根柱子上都有圆盘,所以分两种特殊情况,from的柱子是空的,和to的柱子是空的。
如果from的柱子是空的,那么我们就没有要移动的圆盘,所以这种情况应该直接返回False。
如果to的柱子是空的,那么任何圆盘都可以放在这根柱子上,所以应该直接返回True(排在判断from为空后面)
保证了两根柱子都有圆盘之后,才能通过比较圆盘大小来判断。
最后经过一番折腾写出了个CanMove1
CanMove[stat_, pos_] := stat[[pos[[1]]]] != 0 && (stat[[pos[[2]]]] == 0 || LessEqual @@ LowBit[(Part[stat, #]) & /@ pos]);
Move
其实命名为Move的时候我是觉得有点不妥的,因为这个词太常用了,而且意思太广,即便它不是内置函数也不是关键字,我也觉得用这个词不太好,因为太有可能歧义了,但是我英语水平不行,也不认识其他词,所以还是用Move了。
Move的流程很简单
- 通过
LowBit获取from柱的最小圆盘,作为移动圆盘 - 复制一份当前状态,作为目标状态
- 目标状态的
from柱减去移动圆盘 - 目标状态的
to柱加上移动圆盘 - 返回边,当前状态->目标状态
1 | Move[stat_, pos_] := (x = LowBit[stat[[pos[[1]]]]]; res = stat; res[[pos[[1]]]] -= x; res[[pos[[2]]]] += x; stat -> res); |
生成状态
这里偷懒了,直接用上篇文章的。把之前的dfs复制过来,虽然写的不好但是能跑就先不要动,1
dfs[stat_, n_] := If[n == 0, {stat}, Flatten[Map[(dfs[#, BitShiftRight[n, 1]]) &, n*IdentityMatrix[3] + Table[stat, 3]], 1]];
然后再封装一个生成n个圆盘的所有状态的函数1
Gen[n_] := dfs[{0, 0, 0}, BitShiftLeft[1, n - 1]];
主函数
再看看之前说的那段话,
主要流程就是,对于
S中的每一个状态,对于每一个规则,判断能否通过规则集移动,对于可以移动的,应用对应规则获取边。
一句一句来看,“对于S中的每一个状态,对于每一个规则”,用MMA来写就是Tuples[{S, R}],其实就是S和R的笛卡尔积。
“判断能否通过规则集移动,对于可以移动的”,这里其实换个说法比较好,“选择其中可以移动的”,用MMA写就是Select[Tuples[{S, R}], CanMove[#[[1]], #[[2]]] &],就很生动形象。
最后,“应用对应规则获取边”,这里我用了MMA的符号缩写,至此整个函数已经完成了,就像下面这样
1 | HNT[S_, R_] := Move @@@ Select[Tuples[{S, R}], CanMove[#[[1]], #[[2]]] &]; |
完整代码的截图
画图实验
现在来实验一下,用新编写的代码来画一下图,看和之前的一不一样。
经典汉诺塔问题
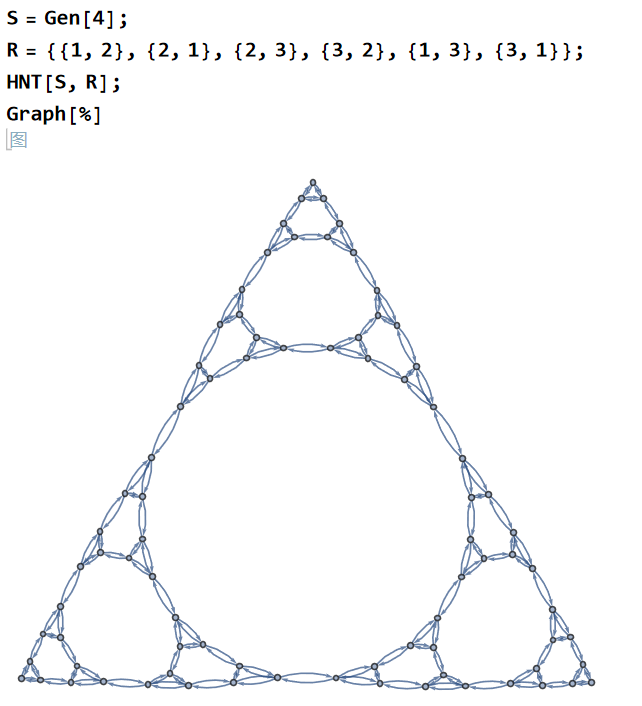
可以发现这个画出来是有向图,之前的是无向图,不过在经典规则的汉诺塔问题下问题不大,因为每个状态之间的关系都是可逆的。
相邻移动的汉诺塔问题
这个图其实一开始我画出来的时候还很不敢相信,因为是一条直线,我差点都怀疑我的代码写错了,直到我输出边信息并且减少圆盘数我才看出原因。

突然就理解了之前题目说的将n个圆盘从第一根柱子移动到第三根柱子上会出现n个圆盘的所有合理摆放是什么意思了。这个过程是线性的,要从左到右把所有状态都走一遍,其实我之前在得出要移动$3^n-1$步,并且总共有$3^n$个状态时就应该想到的,因为移动中不可能出现重复的状态。果然还是画出图更加清晰。
单向移动的汉诺塔问题
这道题之前文章没写,我先拿来画图用了。
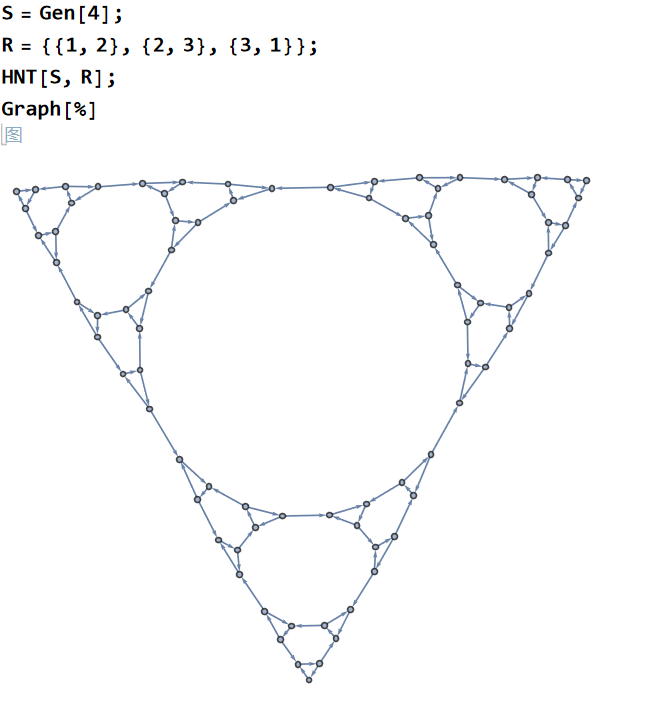
大体上和经典汉诺塔问题的图形状一样,但是正如之前说的,这是有向图,仔细一看会发现大三角形的顶点之间都不能通过直边直接连通,都要曲线救国。
总结
这篇比起汉诺塔问题,其实更多的是我在练习mathematica的使用。虽然我最喜欢的语言还是C++,而且我还是会说,如果用C++我会写得更快更好,但是偶尔换换口味还是挺好的。
这次代码我觉得写得最好的就是1
HNT[S_, R_] := Move @@@ Select[Tuples[{S, R}], CanMove[#[[1]], #[[2]]] &];
感觉写得非常巧妙,很有表达力,这就是函数式编程的魅力,写出这样的代码真的很让人激动。
不过看Move函数的代码还是能看出那是过程式编程的思想,我已经想尽力避免这种写法了,但是还是没有办法,我想不到更好的写法了。