Peano公理的C++模板表示

最近又突发奇想，想整点有趣的活，所以就想用C++的模板来描述一下Peano公理。

为什么使用C++模板

有这么多编程语言，而且我会用的也不少，熟练使用的也有三四种，但是我用C++，准确来说是C++中的模板元编程来描述，除了因为模板元编程写起来很好玩以外，我觉得模板元编程的写法和思想比如模板的特化和递归就很适合用来表示形式化的Peano公理。

什么是Peano公理

Peano公理是一种定义自然数的标准方法，它由以下五条公理组成：

0是自然数
一个自然数的后继数也是自然数
0不是任何自然数的后继数
不同的自然数有不同的后继数，如果两个自然数的后继数相同，则认为这两个自然数相等
（数学归纳原理）令P(n)表示自然数n的任意一个性质，如果P(0)为真且P(n)为真时对于n的后继数也一定为真，那么对于任意自然数n，P(n)一定为真。

准备工作

在开始写代码前，需要做一些准备，才能进行我下面的工作。

需要一个至少支持C++20的编译器
一个带有静态诊断的IDE或者代码编辑器

因为C++是一门不断进化的语言，一些C++20的特性能够让模板元编程更加便捷或者安全，其实不使用C++20也能实现大部分的目标，但是为了看起来更加完美，所以我还是使用了一些C++20的特性。

为什么需要一个带静态诊断的代码编辑器，因为这个东西写出来就是一个玩具，而且编译出来运行其实很没有意义，所以我写这个东西的时候就没有想过要编译。当然这并不是说写出来的东西编译不能通过，而是我们写的东西是更加严密的，是能够在编译期判断正确性的，所以我们可以直接通过静态诊断来更加方便的查看和验证结果。

C++模板描述自然数

首先随意创建个.cpp文件，加入一个用于辅助模板元编程的头文件，然后就可以正式开始我们的工作了。

1	#include<type_traits>

因为我们要做的是定义自然数，所以先定义空的类来表示自然数，这种写法在模板元编程中非常常见，定义一个空类就是用于提供一个符号，不储存任何数据。

1	struct nature{};

这里也只是提供了一个自然数的符号，还没有给它任何定义。给出了自然数的符号，接下来就是如何表示“是自然数”这个概念呢。

我的想法是使用继承，如果一个类继承自nature，那就表示“是自然数”。同时，借助C++20的语法，我们可以用concept来约束类型，用以表示“是自然数”

1 2	template<typename T> concept is_nature = std::is_base_of_v<nature, T>;

这里定义的is_nature就是用来约束类型T，std::is_base_of_v<nature, T>的意思就是nature是T的基类，即T继承自nature，那就它就满足“是自然数”这个概念，

代码层面的准备工作也做完了，接下来看看第一条公理。

0是自然数

现在我们也只把0当成一个符号，而不是我们熟悉的具有什么性质的数，所以我们也给0定义一个符号，之后让我们定义的zero继承自nature，就完成了第一条公理的描述。

1	struct zero: nature{};

非常的简洁而又优雅。

一个自然数的后继数也是自然数

之后我们使用模板来定义后继数，首先后继数也是一个符号，它接受一个模板参数T，表示它是T的后继数，且这个T是自然数，那么后继数也是自然数。

1 2	template<is_nature T> struct succ: nature{};

is_nature T用于约束T是自然数。模板类succ<T>表示T的后继数。succ继承自nature表示它也是自然数。

因为挺多地方都习惯把后继的符号定义为++，刚好C++支持重载运算符，所以我们也来重载一下后继运算符。

template<is_nature T>
constexpr succ<T> operator++(T,int){
    return succ<T>{};
}

注意C++中有两种++运算符，分别是前置和后置，后置++的重载要加一个int参数，之后我们就可以用下面的方法实验一下。

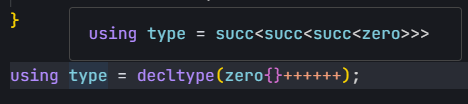
当然上面那个是写模板元编程写魔怔了的写法，也可以使用下面这种看起来正常一点的写法

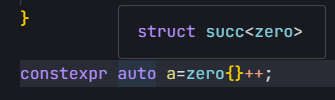
可以看到++运算符确实能用来表示后继数，所以这一步算是完成了。

0不是任何自然数的后继数

其实代码描述的部分到上面就已经结束了，上面的代码已经满足了全部的5条定理了。我认为的后面3条定理其实都是为了数学归纳法服务的，也就是第五条，所以快速带过一下。

0不是任何自然数的后继数。计算机保存整数可能会溢出，发生溢出的话可能会出现后继溢出到0的情况，但是用符号定义的后继数不会产生这个问题，而且zero不会匹配为succ<T>，所以保证了0不是任何自然数的后继。我认为这个是用于确定数学归纳法的递归终止条件的，确保在0的时候终止，不会无限递归。

不同的自然数有不同的后继数

不同的自然数有不同的后继数，如果两个自然数的后继数相同，则认为这两个自然数相等。这个定理应该可以分为两部分，前一部分是用于确保数学归纳法递归路径的唯一性，且能够不重复不遗漏（甚至是不循环）的遍历所有自然数。

后一部分是用于提供递归的判断自然数相等的方法，需要结合第三条公理，这个最终会递归到0=0，即为自然数相等，如果是0=后继数，则与第三条公理矛盾，两个自然数不相等，其实也有一点数学归纳法的味道。

但是在C++中succ<zero>和succ<succ<zero>>天生不是一个类型，每个数都是一个不同的符号不同的类型（当然如果你想的话也可以用其他方法定义它们是同一个类型），且C++可以判断类型相同，所以不需要用这种递归的方式来判断。

当然，如果你非要这么写也不是不行，直接贴代码，不解释。

// 自然数相等的递归定义
template<is_nature N, is_nature M>
constexpr auto equal(succ<N> n,succ<M> m){
    return equal(n,m);
}
// 任何自然数的后继不等于0
template<is_nature N>
constexpr auto equal(succ<N>,zero){
    return false;
}

// 0不等于任何自然数的后继
template<is_nature N>
constexpr auto equal(zero,succ<N>){
    return false;  
}

// 0等于0
constexpr auto equal(zero,zero){
    return true; 
}

数学归纳法

令P(n)表示自然数n的任意一个性质，如果P(0)为真且P(n)为真时对于n的后继数也一定为真，那么对于任意自然数n，P(n)一定为真。

直接看这个东西可能不好理解，在后面看到怎么定义加法的时候就好理解了，正如我上面说的，数学归纳法是一个递归的过程，P(0)提供终止条件，P(n++)是把递归链起来用的。

在这里我先举一些可能不是很好但是非常显然的例子。

如何证明任意自然数都有后继数，首先需要证明0有后继数，然后假设n有后继数succ<n>，之后证明succ<n>也有后继数，这样我们就能证明任意自然数都有后继数了。

如果要证明任意自然数都是0的后继数，就会在第一步卡住，因为0没有后继数。

如果要证明任意自然数，要么是0要么能用0的后继数表示，0的时候显然为真，如果n能用0的后继数表示，n的后继数显然也能用0的后继数表示，所以任意自然数要么是0要么能用0的后继数表示。

结束

这一篇博客就写到这里了，已经实现了Peano公理了，加法下一篇再写。