lean4编写gcd

安装完lean4，当然要试着用一下，由于我也快两年没碰算法了，所有算法几乎都忘完了，就只记得GCD了，所以就写个GCD吧。某种程度上选择GCD说不定刚好，够经典，够简单，够数学。

写在前面

事先声明，我也只是看过一点点教程，还没接触到lean4的皮毛，下面写的都是我自己在试错瞎写的，不报错之后我就端出来了，可能并不标准。

GCD

GCD就是最大公约数，其实就是写个欧几里得算法，也叫辗转相除法，相信大家学过C语言的应该都见过或者写过类似下面这样的代码

int gcd(int a,int b){
    if(b==0)return a;
    else return gcd(b,a%b);
}

非常的简单，算上声明总共就两行，还是个经典的递归函数，通过不断交换和取余，当余数为0的时候，另一个数就是最大公约数。

lean4编写gcd

接下来用lean4来写一下，我编写时使用的是Nat类型，即自然数（零和正整数），这里应该用不到负数，将上面的C语言版本修改一下，大概是下面这样

def gcd(a b:Nat) : Nat :=
  if b = 0 then a else gcd b (a % b)

一些需要注意的地方：

1. lean4是后置类型，以及同一个类型的参数可以写在一起，共享同一个后置类型
2. lean4的函数调用不需要用括号把参数括起来，只需要把参数按顺序写在后面，用空格隔开
3. 因为不需要括号，为了区分参数，需要把一个整体括起来作为一个参数，如上面的(a%b)是一个整体，而不是gcd(b,a)%b

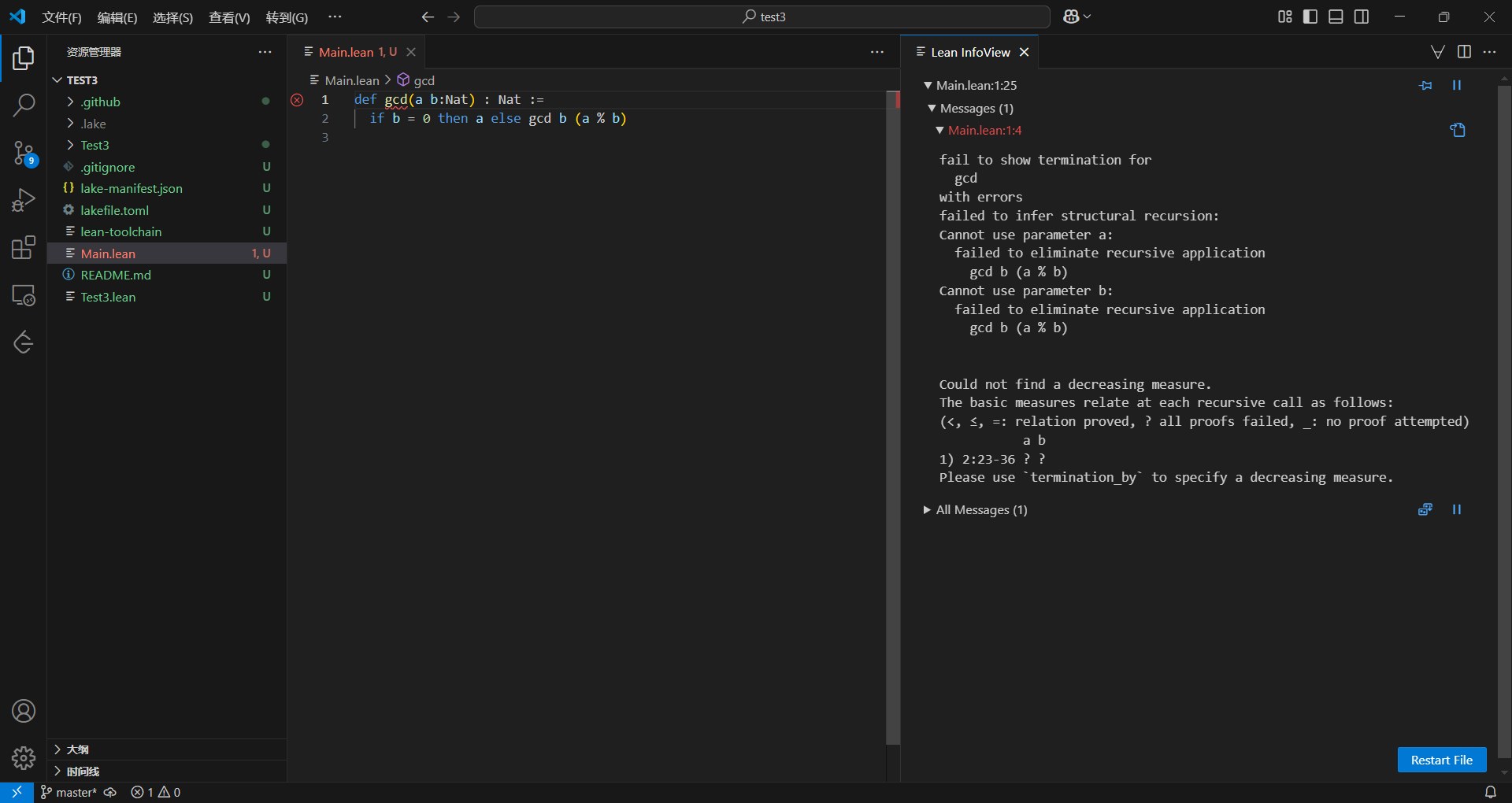
没错，不出意外的出意外了，看右边有一堆字，大概就是说要指定一个会递减的量，来证明递归会终止。我之前看网上说的都是用(a,b)有序对来作为递减度量，但是我觉得只用一个b就行了（我代码中的终止条件是b为0）。所以加上

def gcd(a b:Nat) : Nat :=
  if b = 0 then a else gcd b (a % b)
termination_by b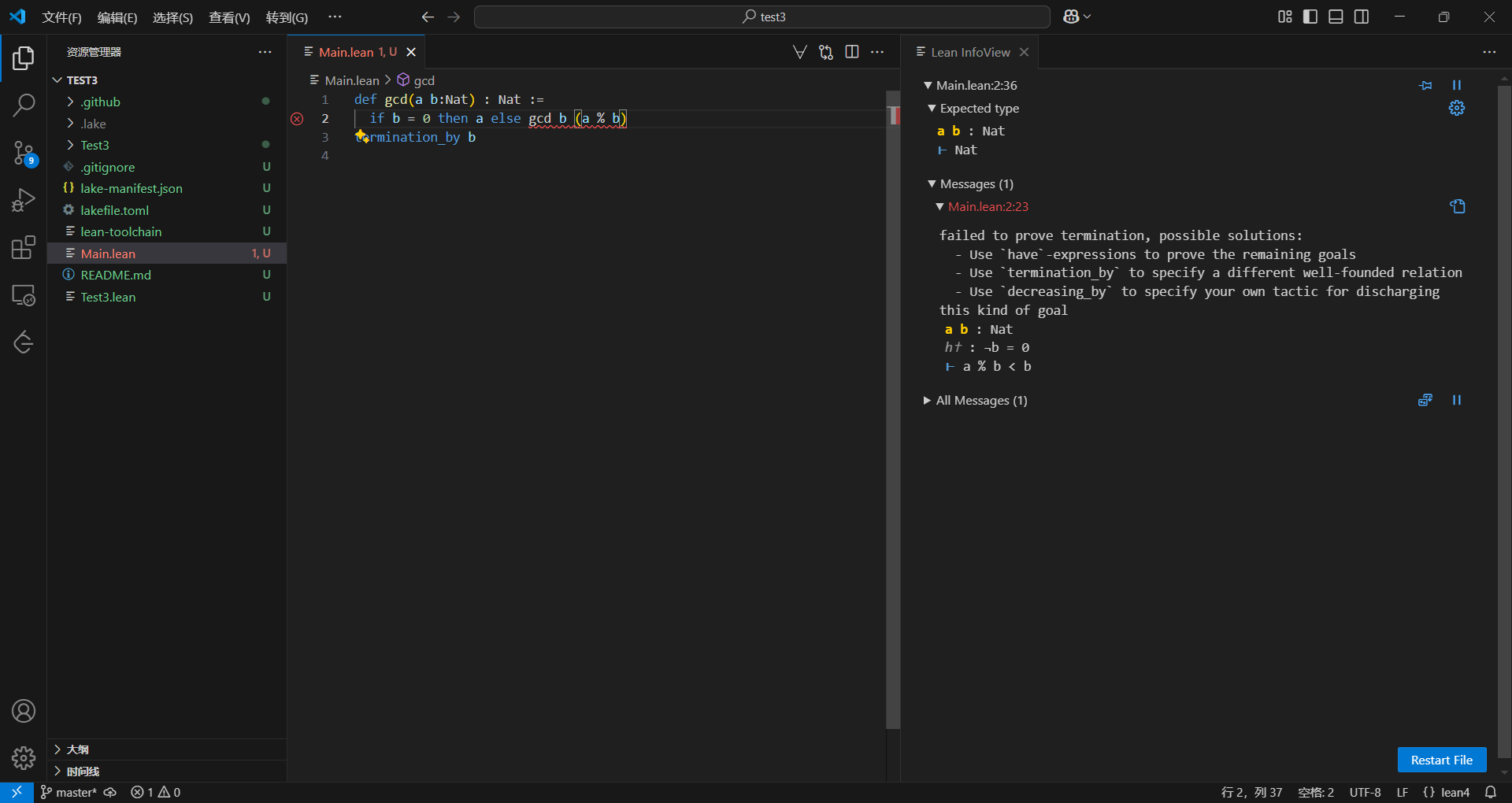

这次右边变得有点颜色了，也开始变得有意思了，大概就是说要证明a%b<b，也就是我们的递归的参数的范围，即第一次是gcd a b的话，第二次就是gcd b a%b，我们选择b（即第二个参数）作为递减度量，那么就需要证明第二个参数在递归的过程中是会不断减小的，避免无限递归，这就是lean4的严谨性。

虽然这个东西我们看起来非常的显然，但是居然不能自动证明了，还需要我们手动证明，接下来就手动证明gcd是停机的。

lean4证明gcd

首先简单说一下右边的证明面板，那个蓝色的分叉标记后面的就是我们要证明的目标，它上面那些黄色的就是我们能够使用的前提条件，我们可以通过使用各种策略和定理来改变目标或者创造条件，最终把目标消除掉就算证明了，跟游戏一样好玩，至于有什么策略和定理就自己去摸索和尝试吧，建议先玩自然数游戏（NNG）入门。

接下来正式开始，目标需要证明a%b<b，我们就先直接让它成立，

def gcd(a b:Nat) : Nat :=
  if b = 0 then a else
  have:a%b<b:=by sorry
  gcd b (a % b)
termination_by b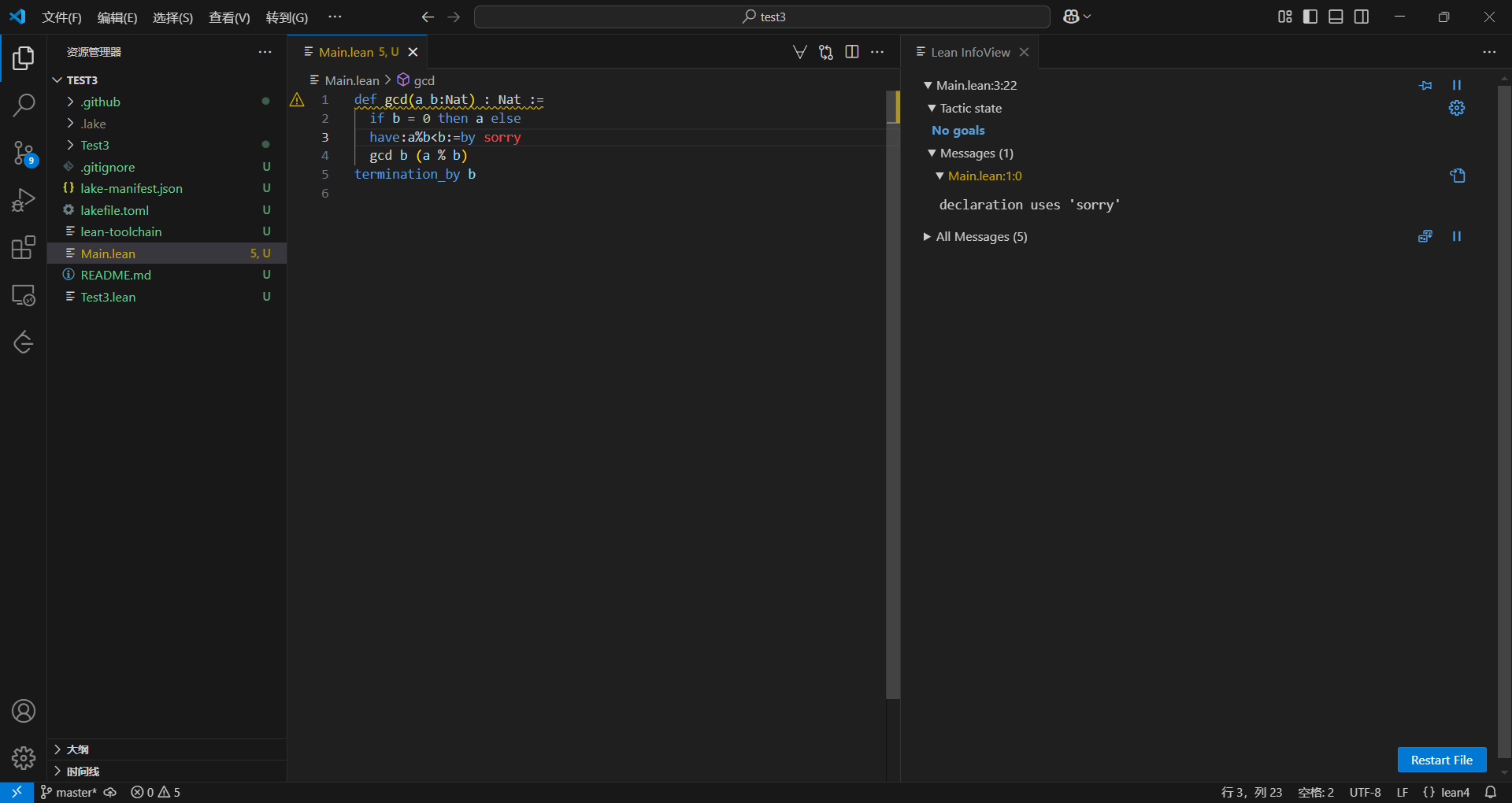

换了一下行，不然一行太多东西了，可以看到现在已经没有报错了，报错变成了警告，说我们使用了sorry，这个的意思大概就是抱歉我不能给出证明，但是它就是成立的。这是一门严谨的语言，肯定是不能这样的，但是我们在开始证明之前都可以先通过这样的方式分解问题，来看能否成立，就像现在加入了这个之后函数已经没有报错了，所以我们只要证明了a%b<b，就相当于证明了gcd是停机的。

之后在Nat的库里面到处翻找，找到了一个形式跟这个一模一样的东西

def gcd(a b:Nat) : Nat :=
  if b = 0 then a else
  have:a%b<b:=by apply Nat.mod_lt
  gcd b (a % b)
termination_by b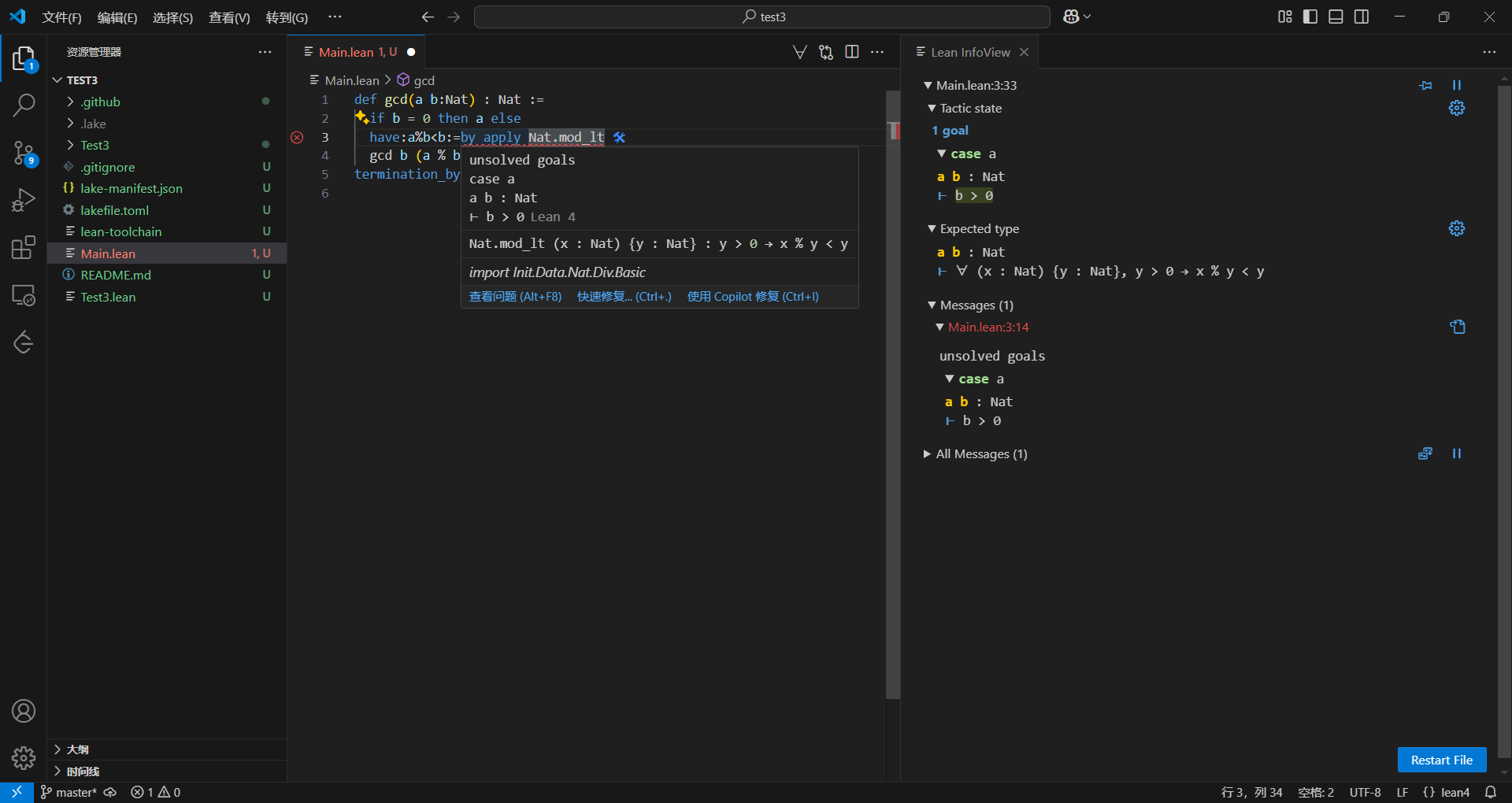

可以看到这时候右边的目标变成了证明b>0，这个是使用这个定理的条件，要使用这个定理需要b>0。根据我们小学的知识，不难发现，自然数都大于等于0，b不等于0的话一定大于0，这个定理的名字说实话我也不知道，也是找了半天找到的，翻译一下意思就是零小于由不等于零推出，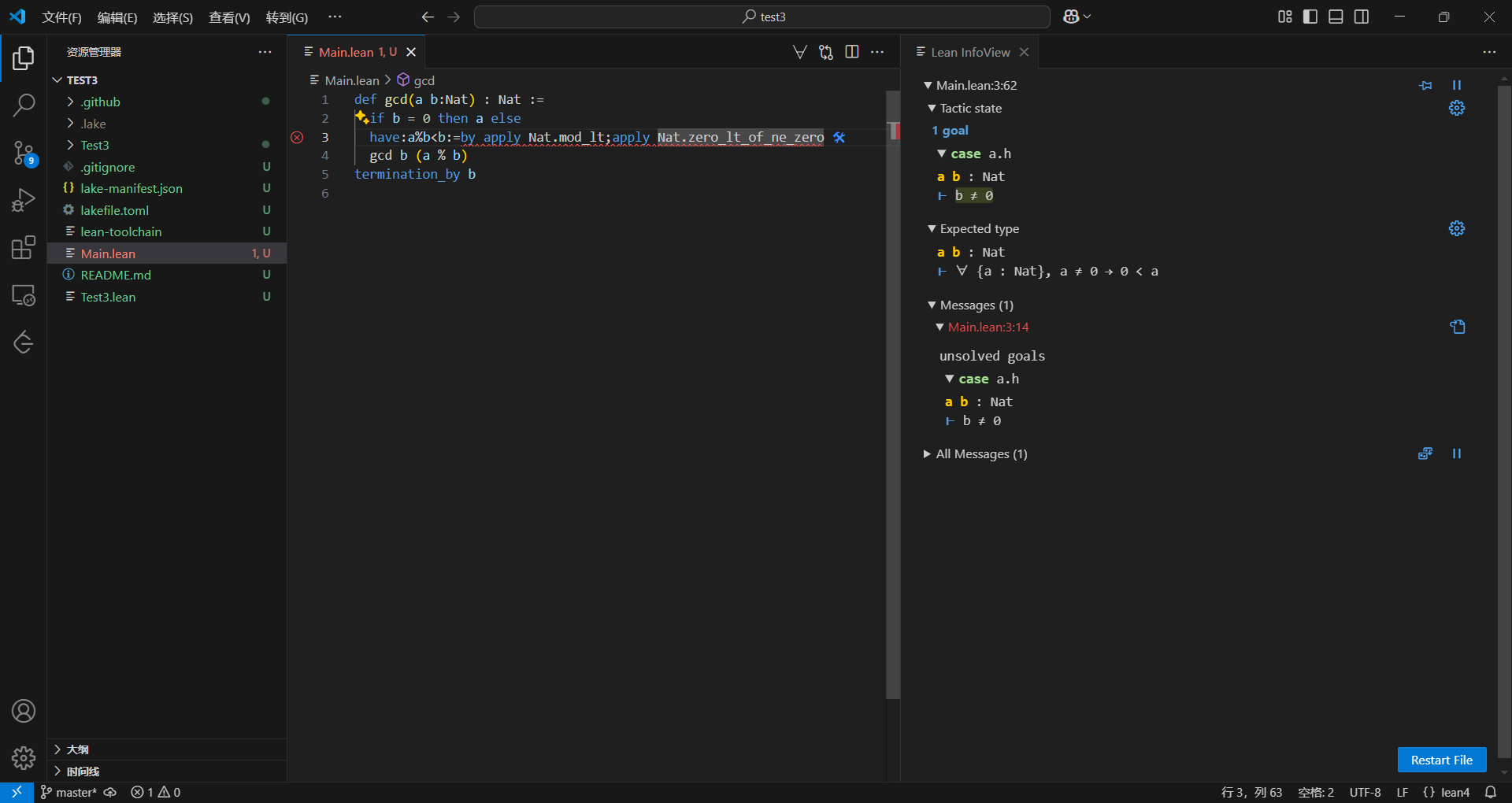

现在需要证明b!=0，这个已经是非常显然的东西了，根据我们前面的假设，这里的b一定不等于0，等于0的不在这个分支，但是这里没有捕获到if那里的假设，所以我们手动捕获一下，给它个名字就行了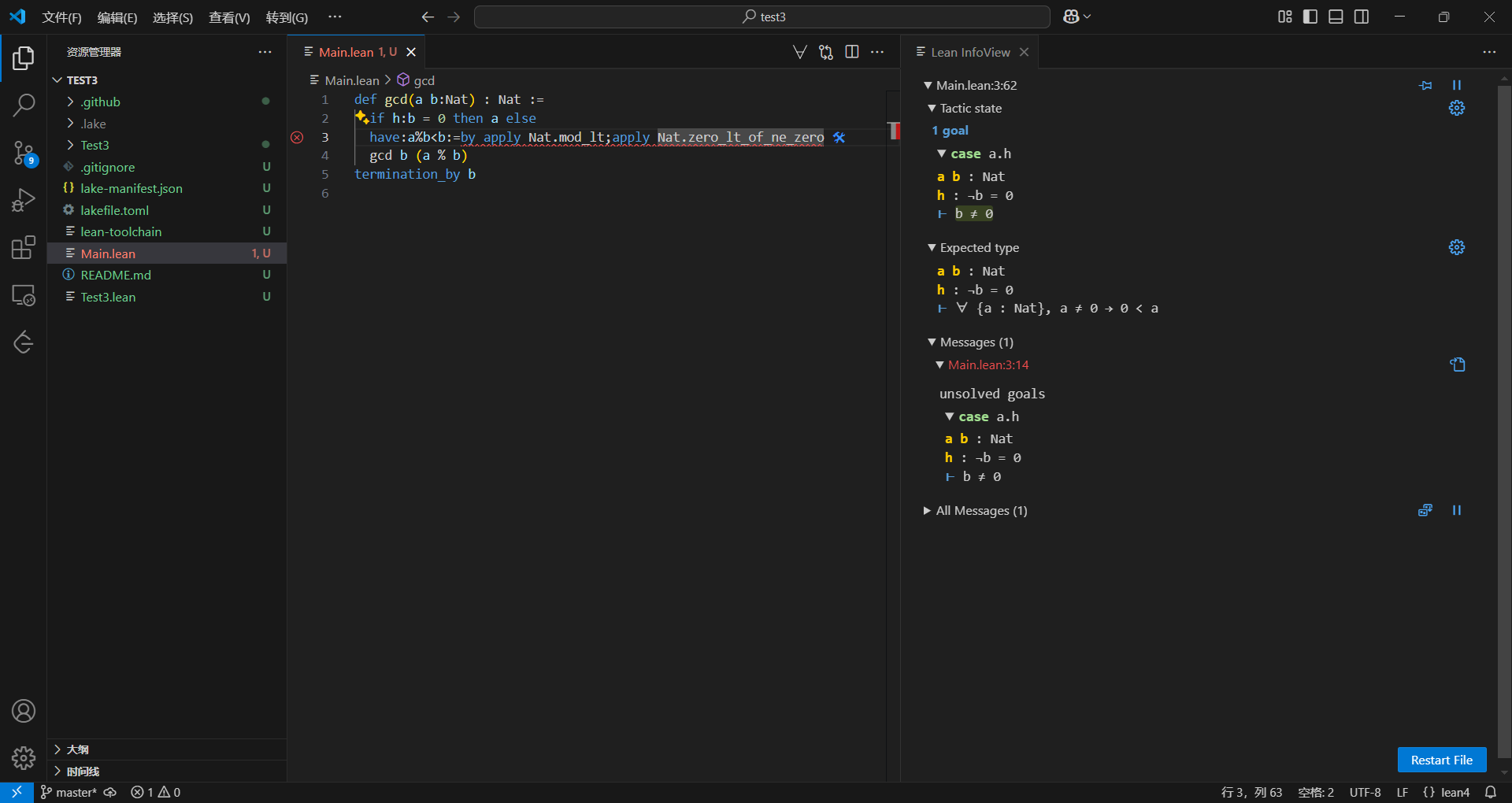

可以看到条件多了一个h，就是我们刚刚加的，在else分支里面是非(b=0)，也就是b!=0，接下来直接在后面加上h就大功告成了

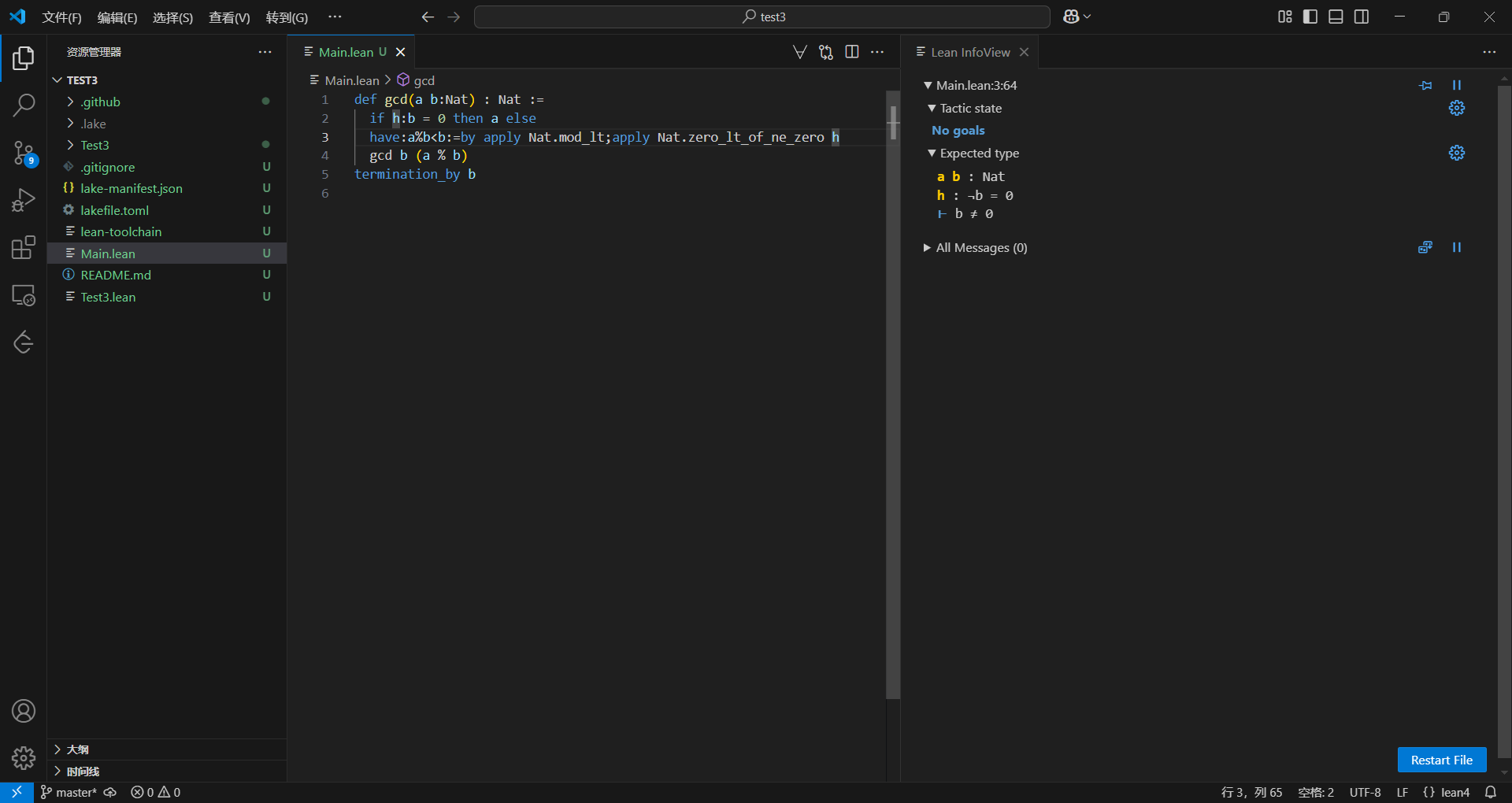
非常的完美，没有报错，然后随便写两个数运行一下试试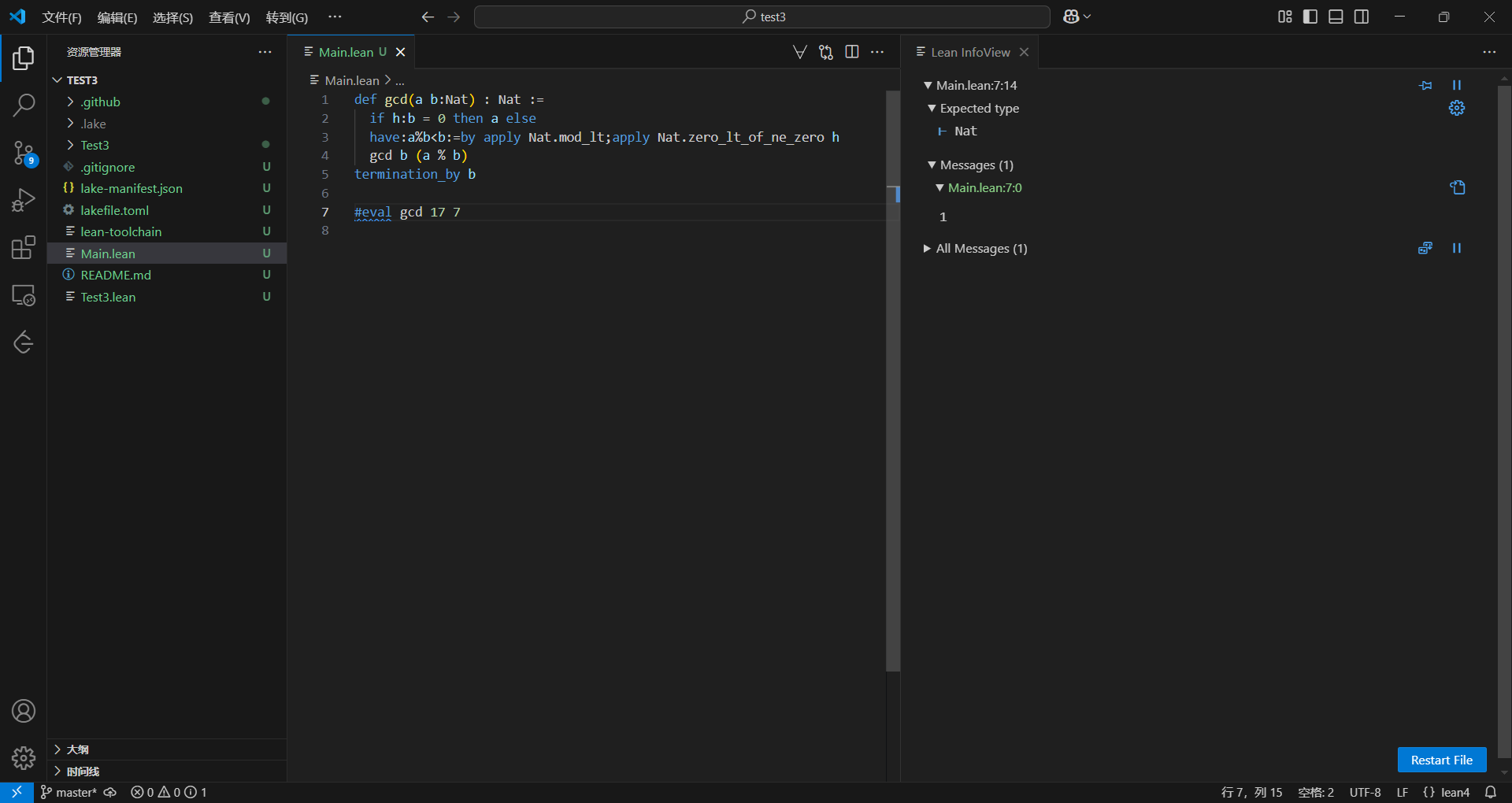

两个经典的质数，结果正确。