lean4证明欧几里得算法

由于前段时间接触了一下lean4，所以就想着能不能用lean4来证明一下欧几里得算法能够求出最大公约数。

开头感想

欧几里得算法可以说是认识了很多年了，从高中刷算法题的时候刷过，到刚上大一的C语言课，到大二的信息安全数学基础，再到大三的密码学，老师还在讲这个算法。

我也不能一直停留在使用上（虽然貌似也好久没有看见什么地方会用这么简单的算法了），也该想想为什么欧几里得算法能够求出最大公约数了，或者说除了用具体数字验算，还有没有什么办法能够证明欧几里得算法算出来的数是两个数的最大公约数。

刚好用lean4来试一下能否形式化证明欧几里得算法能够求出两个数的最大公约数。

最大公约数的定义

最大公约数，首先它要是两个数的公约数，然后它要是所有公约数中最大的。

那么什么是公约数呢，它能同时整除这两个数，假设这两个数为a和b，公约数为n，在编程中的写法是这样

1	a%n==0 && b%n==0

一般读作a模n余数为0，且b模n余数为0。

数学一点的写法是这样

1	n ∣ a ∧ n ∣ b

读作n整除a，且n整除b。说实话接触编程比较早的一开始一直记混这个整除的写法和顺序。

所以我们可以先在lean4中定义一个公约数的概念

1 2	def is_cd (n a b : Nat) : Prop := n ∣ a ∧ n ∣ b

读作：n是a和b的公约数，当n整除a，且n整除b。

然后就是最大公约数的定义，

1 2	def is_gcd (n a b : Nat) : Prop := (is_cd n a b) ∧ ∀ m : Nat, (is_cd m a b) → m ≤ n

应该很好理解，n是a和b的最大公约数，当n是a和b的公约数，且对于任意自然数m，如果m是a和b的公约数，那么m ≤ n（即最大）。

证明欧几里得算法的结果是最大公约数

首先先来写个简单的欧几里得算法，为了防止顶掉标准库里的gcd，我们自己写的这个就叫mygcd了

def mygcd(a b:Nat) : Nat :=
  if h:b = 0 then a else
  have:a%b<b:=by
    apply Nat.mod_lt
    apply Nat.zero_lt_of_ne_zero h
  mygcd b (a % b)
termination_by b

还是老配方，常规的gcd，末尾指定b作为递减度量，然后have提供了证明了b递减的证明。

然后写一个命题表示mygcd是gcd

1	theorem mygcd_is_gcd(a b:Nat): is_gcd (mygcd a b) a b := by sorry

证明的时候我们首先应该先展开is_gcd的定义，然后这是个合取式，可以拆分成两个目标分别证明，甚至可以另外再写出两个命题，像下面这样。

theorem mygcd_is_cd (a b : Nat) : is_cd (mygcd a b) a b := by sorry

theorem cd_le_mygcd(a b:Nat): ∀ m, is_cd m a b → m ≤ mygcd a b := by sorry

theorem mygcd_is_gcd(a b:Nat): is_gcd (mygcd a b) a b := by
  unfold is_gcd
  apply And.intro
  · apply mygcd_is_cd
  · apply cd_le_mygcd

这时候应该能看见mygcd_is_gcd前面打了个大大的勾，说明证明成立，接下来只需要把我们刚刚写的两个命题的sorry换成证明就行了。

证明欧几里得算法的结果是公约数

lean4怎么说也是个交互式定理证明助手，而交互显然是个动态的过程，这就注定了它不能很好的记录在文章里，每一步都把代码和目标截图下来太麻烦了，直接贴代码又不能看到中间的前件和目标的变化（这很重要），所以如果感兴趣的一定要自己一行行敲一遍感受一下。

但是我是个懒人所以我选择直接贴代码

theorem mygcd_is_cd (a b : Nat) : is_cd (mygcd a b) a b := by
  unfold is_cd mygcd
  simp
  by_cases h_b : b = 0
  · rw [h_b]
    apply And.intro
    · exact Nat.dvd_refl a
    · exact Nat.dvd_zero a
  · have:a % b < b := by
      apply Nat.mod_lt
      apply Nat.zero_lt_of_ne_zero h_b
    have:(if b = 0 then a else mygcd b (a % b)) = mygcd b (a % b):=by
      apply if_neg
      exact h_b
    rw [this]
    have ih : is_cd (mygcd b (a % b)) b (a % b) := mygcd_is_cd b (a % b)
    unfold is_cd at ih
    apply And.intro
    · have: mygcd b (a % b) ∣ a % b → mygcd b (a % b) ∣ a := by
        rw [Nat.dvd_mod_iff]
        intro h
        · exact h
        · exact ih.left
      apply this
      exact ih.right
    · exact ih.left
termination_by b

说实话我能人脑进行C++模板元编程，但是没有右边面板的话我还真不能想象出这段代码每一步的前件和目标的变化，但是这段代码只要粘贴到lean4的编辑器里就会直接告诉你这是正确的。

简单说明一下，这个命题的证明也是递归的，关键就是ih那里。以及因为是递归的，所以跟mygcd一样，也指定了递减度量，并且证明了递减。相对的，我们编写mygcd时，对b进行了if分支判断，在证明时就用by_cases对b进行了分类讨论。

证明欧几里得算法的公约数是最大的

证明的过程中发生了一些意外，一个令人绝望的情况，大概是这样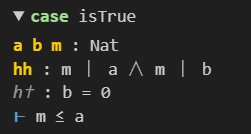

可能这样看起来还不明显我再往下写一点

很显然不成立了，首先相信lean4是不会在这么简单的问题上出错的，然后来找一下问题，这个是当a=0，b=0的时候不成立，我们计算一下#eval mygcd 0 0是0，但是如果按照is_cd的定义，任意自然数都能整除0，任意自然数都能是0和0的公约数，就不能满足m ≤ n。

但是我们稍微思考一下都会知道当a=0，b=0的时候应该是没有意义的，所以问题应该出在这里。

0和0的最大公约数是0！

然后我在网上查了一下，虽然每个地方对于最大公约数都是定义在正整数上的，但是

在现代数学的标准约定中，为了理论完整性和公式统一，定义gcd(0,0)=0。

那这还有什么好说的，但是这样的话我最大公约数应该怎么定义，难道也给0开个特例，这样写起来就太丑陋了，然后我继续找又找到了最大公约数的另一种定义。

最大公约数的正确定义

用lean4写大概是这样的

1 2	def is_gcd (n a b : Nat) : Prop := (is_cd n a b) ∧ ∀ m : Nat, (is_cd m a b) → m ∣ n

前面跟我的一样没什么好说的，主要是后面，如果m是a和b的公约数，那么m能整除n。

如果带入一下0和0貌似确实没毛病，但是为什么是这样定义的，然后让AI找了一下部分高校课本中关于最大公约数的定义，好像确实也都是用的后面这种定义方式，后面截取AI的回答，看如何理解吧

为什么这是”最大”的

在整除关系形成的偏序集中：

· 我们说 d₁ ≤ d₂ 当且仅当 d₁ ∣ d₂

· 最大公约数就是这个偏序集中的最大元素

所以 ∀ m, (is_cd m a b) → m ∣ n 正好表达了 n 是所有公约数的上界，因此是最大的。

所以就先按这个写吧。

公约数整除最大公约数

对原本的命题稍作修改就得到了新的最大性条件，然后证明如下

theorem cd_dvd_mygcd(a b:Nat): ∀ m, is_cd m a b → m ∣ mygcd a b := by
  intro m hh
  unfold is_cd at hh
  unfold mygcd
  simp
  split
  · exact hh.left
  · rename_i hb
    have:a % b < b := by
      apply Nat.mod_lt
      apply Nat.zero_lt_of_ne_zero hb
    have ih: ∀ m, is_cd m b (a%b) → m ∣ mygcd b (a%b) := cd_dvd_mygcd b (a % b)
    apply ih
    unfold is_cd
    apply And.intro
    · exact hh.right
    · rw [Nat.dvd_mod_iff]
      exact hh.left
      exact hh.right
termination_by b

同样也是个递归的命题，用整除定义的最大性条件就很好证明了。

证明完毕

最后修改我们的最大公约数定义，这样就证明完毕了，完整代码如下

def mygcd(a b:Nat) : Nat :=
  if h:b = 0 then a else
  have:a % b < b := by
    apply Nat.mod_lt
    apply Nat.zero_lt_of_ne_zero h
  mygcd b (a % b)
termination_by b

def is_cd(n a b:Nat) : Prop :=
  n ∣ a ∧ n ∣ b

def is_gcd(n a b:Nat) : Prop :=
  is_cd n a b ∧ ∀ m, is_cd m a b → m ∣ n

theorem mygcd_is_cd (a b : Nat) : is_cd (mygcd a b) a b := by
  unfold is_cd mygcd
  simp
  by_cases h_b : b = 0
  · rw [h_b]
    apply And.intro
    · exact Nat.dvd_refl a
    · exact Nat.dvd_zero a
  · have:a % b < b := by
      apply Nat.mod_lt
      apply Nat.zero_lt_of_ne_zero h_b
    have:(if b = 0 then a else mygcd b (a % b)) = mygcd b (a % b):=by
      apply if_neg
      exact h_b
    rw [this]
    have ih : is_cd (mygcd b (a % b)) b (a % b) := mygcd_is_cd b (a % b)
    unfold is_cd at ih
    apply And.intro
    · have: mygcd b (a % b) ∣ a % b → mygcd b (a % b) ∣ a := by
        rw [Nat.dvd_mod_iff]
        intro h
        · exact h
        · exact ih.left
      apply this
      exact ih.right
    · exact ih.left
termination_by b

theorem cd_dvd_mygcd(a b:Nat): ∀ m, is_cd m a b → m ∣ mygcd a b := by
  intro m hh
  unfold is_cd at hh
  unfold mygcd
  simp
  split
  · exact hh.left
  · rename_i hb
    have:a % b < b := by
      apply Nat.mod_lt
      apply Nat.zero_lt_of_ne_zero hb
    have ih: ∀ m, is_cd m b (a%b) → m ∣ mygcd b (a%b) := cd_dvd_mygcd b (a % b)
    apply ih
    unfold is_cd
    apply And.intro
    · exact hh.right
    · rw [Nat.dvd_mod_iff]
      exact hh.left
      exact hh.right
termination_by b

theorem mygcd_is_gcd(a b:Nat): is_gcd (mygcd a b) a b := by
  unfold is_gcd
  apply And.intro
  · apply mygcd_is_cd
  · apply cd_dvd_mygcd

感想

再次证明了我数学基础有多薄弱，居然连最大公约数的定义都不知道，还折腾半天。以及lean4真的挺好玩的，如果证明题都这么好玩就好了，我差点就想买本小学数学证明题练习来用lean4写了（我的水平也就只能写小学证明题了），如果写现在书上的练习，我可能连实数的定义都不知道，而且我lean4至今没能成功安装mathlib4，所以我的lean4也没有实数定义和一大堆实数和微积分之类的相关定理（跟我的脑子一样空），也就只能写写自然数相关的东西了。